题目内容
14.若函数y=ax+m-1 (a>0,a≠1)的图象在第一、三、四象限内,则( )| A. | a>1 | B. | a>1,且m<0 | C. | 0<a<1,且m>0 | D. | 0<a<1 |
分析 由指数函数的性质结合已知可得a>1且m-1<-1,进一步得a>1且m<0.
解答 解:函数y=ax+m-1 (a>0,a≠1)的图象是把函数y=ax的图象向上或向下平移|m-1|个单位得到的.
∵函数y=ax+m-1 (a>0,a≠1)的图象在第一、三、四象限内,
∴a>1且m-1<-1,得a>1且m<0.
故选:B.
点评 本题考查指数函数的图象变换,考查指数函数的性质,是基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
9.已知$\overrightarrow a=({1,2,3}),\overrightarrow b=({-1,1,x})$,且$\overrightarrow a⊥\overrightarrow b$,则x的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
10.设函数f(x)=sin(ωx+φ)+$\sqrt{3}$cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且f(-x)=f(x),则( )
| A. | f(x)在$({0,\frac{π}{2}})$单调递减 | B. | f(x)在$({\frac{π}{2},π})$单调递减 | ||
| C. | f(x)在$({0,\frac{π}{2}})$单调递增 | D. | f(x)在(0,π)单调递增 |
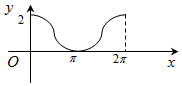
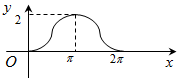
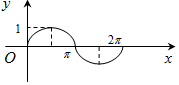
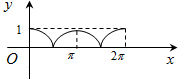
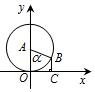 如图,圆A的半径为1,且A点的坐标为(0,1),B为圆上的动点,角α的始边为射线AO,终边为射线AB,过点B作x轴的垂线,垂足为C,将BC表示成α的函数f(α),则y=f(α)在[0,2π]的在图象大致为( )
如图,圆A的半径为1,且A点的坐标为(0,1),B为圆上的动点,角α的始边为射线AO,终边为射线AB,过点B作x轴的垂线,垂足为C,将BC表示成α的函数f(α),则y=f(α)在[0,2π]的在图象大致为( )