题目内容
10.设函数f(x)=sin(ωx+φ)+$\sqrt{3}$cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且f(-x)=f(x),则( )| A. | f(x)在$({0,\frac{π}{2}})$单调递减 | B. | f(x)在$({\frac{π}{2},π})$单调递减 | ||
| C. | f(x)在$({0,\frac{π}{2}})$单调递增 | D. | f(x)在(0,π)单调递增 |
分析 化简函数f(x),根据f(x)的最小正周期为π得出ω的值,根据f(-x)=f(x)求出φ的值,再判断f(x)的增减性.
解答 解:函数f(x)=sin(ωx+φ)+$\sqrt{3}$cos(ωx+φ)
=2sin(ωx+φ+$\frac{π}{3}$),
且f(x)的最小正周期为π,
∴ω=2,
∵f(-x)=f(x),
∴φ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z;
解得φ=kπ+$\frac{π}{6}$,k∈Z;
又|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{6}$;
∴f(x)=2sin(2x+$\frac{π}{2}$)=2cos2x,
∴f(x)在$({0,\frac{π}{2}})$单调递减.
故选:A.
点评 本题考查了三角函数的化简、三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
14.若函数y=ax+m-1 (a>0,a≠1)的图象在第一、三、四象限内,则( )
| A. | a>1 | B. | a>1,且m<0 | C. | 0<a<1,且m>0 | D. | 0<a<1 |
15.函数f(x)=$\frac{ln(x-1)}{\sqrt{4-{x}^{2}}}$的定义域为( )
| A. | (1,2) | B. | [1,2] | C. | (1,4) | D. | [2,4] |
2.已知函数f(x)=|x-2|+|x+2|,则下列坐标表示的点一定在函数f(x)图象上的是( )
| A. | (a,-f(a)) | B. | (a,-f(-a)) | C. | (-a,-f(a)) | D. | (-a,f(a)) |
19.关于x的方程4x-m•2x+1+4=0有实数根,则m的取值范围( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
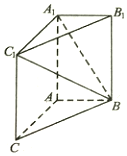 如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.