题目内容
6.已知点P(2,0)及圆C:x2+y2-6x+4y+4=0.(1)若直线l过点P且与圆心C的距离为1,求直线l的方程.
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
分析 (1)分直线斜率存在与否,两种情况解答;
(2)把直线y=ax+1代入圆C的方程d得到关于x的一元二次方程,利用交点个数与判别式的关系得到a的范围,设符合条件的实数a存在,利用直线垂直的斜率关系得到a值判断.
解答 解:(1)设直线l的斜率为k(k存在),则方程为y-0=k(x-2),即kx-y-2k=0.
又圆C的圆心为(3,-2),半径r=3,由$\frac{|3k+2-2k|}{\sqrt{{k}^{2}+1}}$=1,解得k=-$\frac{3}{4}$.
所以直线方程为y=-$\frac{3}{4}$(x-2),即3x+4y-6=0.
当l的斜率不存在时,l的方程为x=2,经验证x=2也满足条件.
综上所述,直线l的方程为3x+4y-6=0或x=2;
(2)把直线y=ax+1代入圆C的方程,消去y,整理得(a2+1)x2+6(a-1)x+9=0.
由于直线ax-y+1=0交圆C于A,B两点,
故△=36(a-1)2-36(a2+1)>0,解得a<0.则实数a的取值范围是(-∞,0).
设符合条件的实数a存在.
由于l2垂直平分弦AB,故圆心C(3,-2)必在l2上.所以l2的斜率kPC=-2.
而kAB=a=-$\frac{1}{{k}_{PC}}$,所以a=$\frac{1}{2}$.
由于$\frac{1}{2}$∉(-∞,0),故不存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB.
点评 本题考查了直线方程的求法以及直线与圆的位置关系的判断;属于中档题.

练习册系列答案
相关题目
17.若全集U={1,2,3,4,5},A={2,4,5},B={1,2,5},则(∁UA)∩B=( )
| A. | {2,5} | B. | {1,3,4} | C. | {1,2,4,5} | D. | {1} |
14.若函数y=ax+m-1 (a>0,a≠1)的图象在第一、三、四象限内,则( )
| A. | a>1 | B. | a>1,且m<0 | C. | 0<a<1,且m>0 | D. | 0<a<1 |
1.圆x2+y2=4与圆x2+y2-6x+8y-24=0的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 内切 | D. | 外切 |
2.已知函数f(x)=|x-2|+|x+2|,则下列坐标表示的点一定在函数f(x)图象上的是( )
| A. | (a,-f(a)) | B. | (a,-f(-a)) | C. | (-a,-f(a)) | D. | (-a,f(a)) |
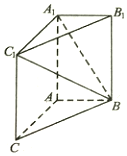 如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.