题目内容
 已知四棱锥S-ABCD,AD∥BC,∠ABC=90°,面SAB⊥底面ABCD,SA=SB=
已知四棱锥S-ABCD,AD∥BC,∠ABC=90°,面SAB⊥底面ABCD,SA=SB=
| ||
| 2 |
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)证明:AB⊥SM;
(Ⅲ)证明:SD∥面AEF.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)取AB的中点O,连结SO,SO⊥AB,SO⊥底面ABCD,由此能求出四棱锥S-ABCD的体积.
(Ⅱ)由已知得SO⊥AB,OM⊥AB,由此能证明AB⊥SM.
(Ⅲ)连结DB交AF于N,连结EN,EN∥SD,由此能证明SD∥面AFE.
(Ⅱ)由已知得SO⊥AB,OM⊥AB,由此能证明AB⊥SM.
(Ⅲ)连结DB交AF于N,连结EN,EN∥SD,由此能证明SD∥面AFE.
解答:
(Ⅰ)解:取AB的中点O,连结SO,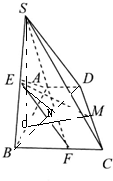
∵SA=SB,∴SO⊥AB,
∵面SAB⊥面ABCD,∴SO⊥底面ABCD,
∵SA=SB=
a,AB=a,
∴SO=
=
a,
∴V=
×
a×
×a×(a+2a)=
a3.
(Ⅱ)证明:连结OM,∵SO⊥底面ABCD,∴SO⊥AB,
∵O,M分别为AB,CD的中点,
∴AD∥OM,∴OM⊥AB,
∴AB⊥面SOM,∴AB⊥SM.
(Ⅲ)证明:连结DB交AF于N,连结EN,
∵AD与BF平行且相等,∴N为DB的中点,
∴EN∥SD,
又SD?平面AFE,EN?平面AFE,
∴SD∥面AFE.

∵SA=SB,∴SO⊥AB,
∵面SAB⊥面ABCD,∴SO⊥底面ABCD,
∵SA=SB=
| ||
| 2 |
∴SO=
|
| ||
| 2 |
∴V=
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
(Ⅱ)证明:连结OM,∵SO⊥底面ABCD,∴SO⊥AB,
∵O,M分别为AB,CD的中点,
∴AD∥OM,∴OM⊥AB,
∴AB⊥面SOM,∴AB⊥SM.
(Ⅲ)证明:连结DB交AF于N,连结EN,
∵AD与BF平行且相等,∴N为DB的中点,
∴EN∥SD,
又SD?平面AFE,EN?平面AFE,
∴SD∥面AFE.
点评:本题考查四棱锥S-ABCD的体积的求法,考查异面直线垂直的证明,考查直线与平面平行的证明,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
高三某班上午有4节课,现从6名教师中安排4人各上一节课,如果甲乙两名教师不上第一节课,丙必须上最后一节课,则不同的安排方案种数为( )
| A、36 | B、24 | C、18 | D、12 |
已知下列命题:
①命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”;
③“a>2”是“a>5”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
①命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1<3x”;
②已知p、q为两个命题,若“p∨q”为假命题,则“¬p∧¬q为真命题”;
③“a>2”是“a>5”的充分不必要条件;
④“若xy=0,则x=0且y=0”的逆否命题为真命题.
其中所有真命题的序号是( )
| A、①②③ | B、②④ | C、② | D、④ |
下列命题中,真命题的是( )
| A、命题“若ac>bc,则a>b” |
| B、命题“若b=3,则b2=9”的逆命题 |
| C、命题“若x=2,则x2-3x+2=0”的否命题 |
| D、命题“相似三角形的对应角相等”的逆否命题 |
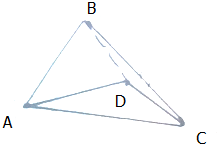 如图,在四面体ABCD中,△ABD是正三角形,AB⊥BC,AD⊥DC,AC=2AB,则直线DC与平面ABD所成角的正弦值等于
如图,在四面体ABCD中,△ABD是正三角形,AB⊥BC,AD⊥DC,AC=2AB,则直线DC与平面ABD所成角的正弦值等于