Question

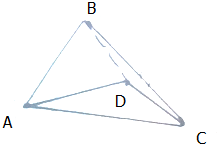如图，在四面体ABCD中，△ABD是正三角形，AB⊥BC，AD⊥DC，AC=2AB，则直线DC与平面ABD所成角的正弦值等于

 

．

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：根据直线和平面所成角的定义，先找出直线DC与平面ABD所成角，利用三角形的边角关系即可求出直线DC与平面ABD所成角的正弦值．

解答： 解：如图所示，
四面体ABCD中，∵△ABD是正三角形，AB⊥BC，AD⊥DC，且AC=2AB；
设AB=a，则AC=2a，∴BC=DC=

3

a；
取BD的中点E，连接CE、AE，
则CE⊥BD，AE⊥BD；
又CE∩AE=E，
∴BD⊥平面ACE，
又BD?平面ABD，
∴平面ABD⊥平面ACE，
过点C作CF⊥AE于F，
则CF⊥平面ABD；
连接DF，则∠CDF就是直线CD与平面ABD所成的角；
∵AB=a，BC=DC=

3

a，
∴AE=

3 a

2

，CE=

( 3 a)2-( a 2 )2

=

11

2

a；
∴cos∠AEC=

AE2+CE2-AC2

2AE•CE

=

3 4 a2+ 11 4 a2-4a2

2× 3 2 a• 11 2 a

=-

33

33

，
∴CF=EC•sin∠AEC=

11

2

a•

1-(- 33 33 )2

=

2 6 a

3

，
∴sin∠CDF=

CF

CD

=

2 6 3 a

3 a

=

2 2

3

即直线DC与平面ABD所成角的正弦值为

2 2

3

．
故答案为：

2 2

3

点评：本题考查了求直线与平面所成角的求解，解题的关键是找出直线与平面所成的角，考查学生的推理和计算能力．