题目内容
16.点E是正方形ABCD的边DC的中点,F是BE中点,且$\overrightarrow{AB}$=$\overrightarrow{a}$.$\overrightarrow{AD}$=$\overrightarrow{b}$.则$\overrightarrow{DF}$=( )| A. | $\frac{1}{2}\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{b}$-$\frac{3}{4}\overrightarrow{a}$ | C. | $\frac{3}{4}\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{a}$ | D. | $\frac{3}{4}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$ |
分析 根据向量加法及数乘的几何意义便可得出$\overrightarrow{DF}=\overrightarrow{DE}+\overrightarrow{EF}$,$\overrightarrow{DE}=\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{EB}=\frac{1}{2}(\overrightarrow{EC}+\overrightarrow{CB})$,$\overrightarrow{EC}=\frac{1}{2}\overrightarrow{AB},\overrightarrow{CB}=-\overrightarrow{AD}$,依次带入前面的式子便可用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{DF}$,即用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{DF}$.
解答  解:如图,根据条件:
解:如图,根据条件:
$\overrightarrow{DF}=\overrightarrow{DE}+\overrightarrow{EF}$
=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{EB}$
=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{EC}+\overrightarrow{CB})$
=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$
=$\frac{3}{4}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$
=$\frac{3}{4}\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$.
故选:D.
点评 考查向量加法和数乘的几何意义,以及向量的数乘运算,相等向量和相反向量的概念.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
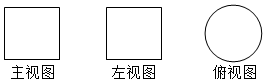 加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.
加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.