题目内容
1.已知一批产品的次品率为P=0.12,从中任取5件,求取得各次品数的概率.分析 一批产品的次品率为P=0.12,从中任取5件,取得各次品数X~B(5,0.12),由此能求出取得各次品数的概率.
解答 解:∵一批产品的次品率为P=0.12,从中任取5件,
∴取得各次品数X~B(5,0.12),
∴恰好取到0件次品的概率:P(X=0)=${C}_{5}^{0}(1-0.12)^{5}$≈0.527732,
恰好取到1件次品的概率:P(X=1)=${C}_{5}^{1}×0.12×(1-0.12)^{4}$≈0.359817,
恰好取到2件次品的概率:P(X=2)=${C}_{5}^{2}(0.12)^{2}(1-0.12)^{3}$≈0.098132,
恰好取到3件次品的概率:P(X=3)=${C}_{5}^{3}(0.12)^{3}(1-0.12)^{2}$≈0.013382,
恰好取到4件次品的概率:P(X=4)=${C}_{5}^{4}(0.12)^{4}(1-0.12)$≈0.000912,
恰好取到5件次品的概率:P(X=5)=0.125≈0.000025.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.点E是正方形ABCD的边DC的中点,F是BE中点,且$\overrightarrow{AB}$=$\overrightarrow{a}$.$\overrightarrow{AD}$=$\overrightarrow{b}$.则$\overrightarrow{DF}$=( )
| A. | $\frac{1}{2}\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{b}$-$\frac{3}{4}\overrightarrow{a}$ | C. | $\frac{3}{4}\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{a}$ | D. | $\frac{3}{4}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$ |
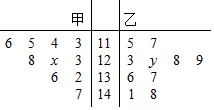 在某校统考中,甲、乙两班数学学科前10名的成绩如表:
在某校统考中,甲、乙两班数学学科前10名的成绩如表: