题目内容
12．
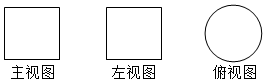加图所示，一个空间几何体的主视图和左视图都是边长为3的正方形，俯视图是一个直径为3的圆，那么这个几何体的全面积为36π．
分析 由三视图得到几何体是底面半径为3，高为3的圆柱，由此计算体积．
解答 解：由题意，几何体是底面半径为3，高为3的圆柱，所以全面积为2π×32+6π×3=36π；
故答案为：36π．
点评 本题考查了几何体的三视图以及几何体的全面积求法；关键是正确还原几何体．
练习册系列答案
相关题目
20．已知△ABC的内切圆与边AB，AC，BC相切于点P，Q，R，若|CR|=1，|AB|=2，则动点C的轨迹曲线的离心率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
16．点E是正方形ABCD的边DC的中点，F是BE中点，且$\overrightarrow{AB}$=$\overrightarrow{a}$．$\overrightarrow{AD}$=$\overrightarrow{b}$．则$\overrightarrow{DF}$=（ ）
| A． | $\frac{1}{2}\overrightarrow{a}$-$\frac{3}{4}$$\overrightarrow{b}$ | B． | $\frac{1}{2}\overrightarrow{b}$-$\frac{3}{4}\overrightarrow{a}$ | C． | $\frac{3}{4}\overrightarrow{b}$-$\frac{1}{2}\overrightarrow{a}$ | D． | $\frac{3}{4}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$ |