题目内容
10.(1)若6x=24y=12,求$\frac{1}{x}$+$\frac{1}{y}$的值;(2)解方程:1og2(2x+8)=x+1.
分析 (1)根据对数的定义,求出x,y,再根据换底公式求出$\frac{1}{x}$,$\frac{1}{y}$,根据对数的运算性质计算即可;
(2)根据对数的定义得到2x+8=2x+1,再根据指数幂的运算求出即可.
解答 解:(1)6x=24y=12,
∴x=log612,y=log2412,
∴$\frac{1}{x}$+$\frac{1}{y}$=log126+log1224=log12(6×24)=log12122=2,
(2)1og2(2x+8)=x+1.
∴2x+8=2x+1=2×2x,
∴2x=8=23,
∴x=3.
点评 本题考查了对数的运算性质和换底公式,以及指数幂的运算,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{5}{4}$,且双曲线C的焦点到它的一条渐近线的距离为3,则双曲线C的方程为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
4.中心为原点,一个焦点为$F(0,5\sqrt{2})$的椭圆截直线y=3x-2所得的弦的中点的横坐标为$\frac{1}{2}$,则椭圆的方程为( )
| A. | $\frac{x^2}{25}+\frac{y^2}{75}=1$ | B. | $\frac{x^2}{75}+\frac{y^2}{25}=1$ | C. | $\frac{{2{x^2}}}{75}+\frac{{2{y^2}}}{25}=1$ | D. | $\frac{{2{x^2}}}{25}+\frac{{2{y^2}}}{75}=1$ |
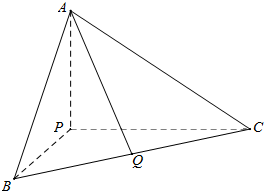 在三棱锥P-ABC中,已知PA,PB,PC两两垂直,PB=5,PC=6,三棱锥P-ABC的体积为20,Q是BC的中点,求异面直线PB,AQ所成角的大小(结果用反三角函数值表示).
在三棱锥P-ABC中,已知PA,PB,PC两两垂直,PB=5,PC=6,三棱锥P-ABC的体积为20,Q是BC的中点,求异面直线PB,AQ所成角的大小(结果用反三角函数值表示).