题目内容
4.中心为原点,一个焦点为$F(0,5\sqrt{2})$的椭圆截直线y=3x-2所得的弦的中点的横坐标为$\frac{1}{2}$,则椭圆的方程为( )| A. | $\frac{x^2}{25}+\frac{y^2}{75}=1$ | B. | $\frac{x^2}{75}+\frac{y^2}{25}=1$ | C. | $\frac{{2{x^2}}}{75}+\frac{{2{y^2}}}{25}=1$ | D. | $\frac{{2{x^2}}}{25}+\frac{{2{y^2}}}{75}=1$ |
分析 根据焦点坐标得出a2-b2=50,将直线的方程与椭圆的方程组成方程组,消去y得到关于x的方程,再根据根与系数的关系求得AB的中点的横坐标的表达式,最后根据联立的方程求出其a,b即可求椭圆的方程.
解答 解:设椭圆的方程为$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=5$\sqrt{2}$,即为a2-b2=50,①
将直线y=3x+2代入椭圆方程,可得
(9b2+a2)x2-12b2x+4b2-a2b2=0,
由弦的中点的横坐标为$\frac{1}{2}$,
设弦的两个端点为A(x1,y1),B(x2,y2),
则由根与系数的关系可得,x1+x2=$\frac{12{b}^{2}}{{a}^{2}+9{b}^{2}}$,
由中点坐标公式可得,$\frac{12{b}^{2}}{{a}^{2}+9{b}^{2}}$=1,
即有a2=3b2②
联立①②可得,a2=75,b2=25
∴椭圆方程为$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{75}$=1.
故选:A.
点评 本题主要考查了椭圆的标准方程、直线与圆锥曲线的综合问题.主要涉及韦达定理、中点坐标公式等.

练习册系列答案
相关题目
9.椭圆满足这样的光学性质:从椭圆的一个焦点发射光线,经椭圆反射后,反射光线经过椭圆的另一焦点.现在设有一个水平放置的椭圆形台球盘,满足方程$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,点A、B是它的两个焦点,当静止的小球放在A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的路程是( )
| A. | 20 | B. | 18 | C. | 2 | D. | 以上均有可能 |
13.定义在(0,+∞)上的函数f(x)满足:f(x)>xf′(x),且f(2)=4,则不等式f(x)-2x>0的解集为( )
| A. | (2,+∞) | B. | (0,2) | C. | (0,4) | D. | (4,+∞) |
 某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.
某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.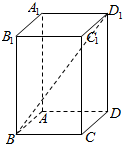 如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.
如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.