在△ABC中.已知A=30°.B=120°.b=5.解三角形．题目和参考答案——青夏教育精英家教网—

题目内容

7．在△ABC中，已知A=30°，B=120°，b=5，解三角形．

分析由三角形的内角和可得C，可得等腰三角形，由正弦定理可得a和c．

解答解：∵A=30°，B=120°，∴C=180°-（A+B）=30°．
∴A=C，∴a=c．由正弦定理可得a=$\frac{bsinA}{sinB}$=$\frac{5sin30°}{sin120°}$=$\frac{5\sqrt{3}}{3}$，
综上可知，C=30°，a=c=$\frac{5\sqrt{3}}{3}$

点评本题考查解三角形，涉及正余弦定理的应用，属基础题．

练习册系列答案

相关题目

12．函数y=ln（ax²+x-1）的值域为R，当且仅当（　　）

13．给出如下说法：
①命题“若x²-3x+2=0，则x=1”的逆否命题是“若x≠1，则x²-3x+2≠0”
②若命题p：?x∈R，x²+x+1=0，则￢p：?x∈R，x²+x+1≠0
③若p∧q为假命题，则p，q均为假命题
④“x＞2”是“x²-3x+2＞0”的充分不必要条件
其中正确命题的序号有①②④．

10．（1）若6^x=24^y=12，求$\frac{1}{x}$+$\frac{1}{y}$的值；
（2）解方程：1og₂（2^x+8）=x+1．

2．已知a＞0，函数f（x）=e^axsinx（x∈[0，+∞））．记x_n为f（x）的从小到大的第n（n∈N^*）个极值点，则数列{f（x_n）}是（　　）

	A．	等差数列，公差为e^ax		B．	等差数列，公差为-e^ax
	C．	等比数列，公比为e^ax		D．	等比数列，公比为-e^ax

12．

某高三年级从甲（文）乙（理）两个年级组各选出7名学生参加高校自主招生数学选拔考试，他们取得的成绩（满分：100分）的茎叶图如图所示，其中甲组学生的平均分是85分，乙组学生成绩的中位数是83分．
（1）求x和y的值；
（2）从成绩在90分以上的学生中随机取两名学生，求甲组至少有一名学生的概率．

19．设数列{a_n}满足a₁=1，a_n+1=3a_n．
（1）求{a_n}的通项公式及前n项和S_n；
（2）已知{b_n}是等差数列，T_n为前n项和，且b₁=a₂，b₂=a₁+a₂+a₃，求T₃₈．

16．

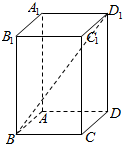如图，在正四棱柱中ABCD-A₁B₁C₁D₁，AB=1，D₁B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$，求该四棱柱的表面积．

17．

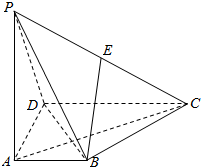如图，在四棱锥P-ABCD中，PA⊥ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．
（1）证明BE⊥DC；
（2）求二面角E-AB-P的值；
（3）求直线BE与平面PBD所成角的正弦值．

试题分类