题目内容
设
，
为非零向量，|
|=2|
|，两组向量
，
，
，
和
，
，
，
均由2个
和2个
排列而成，若
•
+
•
+
•
+
•
所有可能取值中的最小值为4|
|2，则
与
的夹角为 ．
| a |
| b |
| b |
| a |
| x1 |
| x2 |
| x3 |
| x4 |
| y1 |
| y2 |
| y3 |
| y4 |
| a |
| b |
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| b |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：结合数量积组合情况，分类讨论，即可得出结论．
解答：
解：由题意，设
与
的夹角为θ
分类讨论可得
①
•
+
•
+
•
+
•
=
•
+
•
+
•
+
•
=10|
|2，不满足条件，
②
•
+
•
+
•
+
•
=
•
+
•
+
•
+
•
=5|
|2+4|
|2cosθ，不满足条件，
③
•
+
•
+
•
+
•
=
•
+
•
+
•
+
•
=4
•
=8|
|2cosθ=4|
|2，此时cosθ=
∴
与
的夹角为θ=60°，
故答案为：60°
| a |
| b |
分类讨论可得
①
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| a |
| a |
| b |
| b |
| b |
| b |
| a |
②
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| a |
| b |
| a |
| b |
| b |
| b |
| a |
| a |
③
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| 1 |
| 2 |
∴
| a |
| b |
故答案为：60°
点评：本题考查向量的数量积公式，考查学生的计算能力，注意要进行分类讨论．
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
已知复数z的共轭复数是
，则复数z2+
+3等于（ ）
| 2-2i |
| 1+i |
. |
| z |
| A、-2i | B、3-i |
| C、1+2i | D、-1-2i |
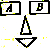用黑、蓝2种颜色给如图所示的笑脸涂色，每个图形只能涂一种颜色，则两只眼睛（即图中A、B所示的区域）涂同种颜色而鼻子和嘴巴涂不同颜色的概率为（ ）