题目内容
17.在△ABC中,角A,B,C所对的边长分别为a,b,c.已知sinA+sinC=psinB(p∈R),且b2=3ac.(Ⅰ)当$p=\frac{4}{3},b=1$时,求a,c的值;
(Ⅱ)若角B为钝角,求p的取值范围.
分析 (Ⅰ)由条件利用正弦定理可得b2=3ac=1,a+c=$\frac{4}{3}$b=$\frac{4}{3}$,由此解得a和c的值.
(Ⅱ)由条件利用余弦定理求得p2=$\frac{5}{3}$+$\frac{2}{3}$cosB,再结合-1<cosB<0,求得p2的范围,从而求得p的范围.
解答 解:△ABC中,∵sinA+sinC=psinB(p∈R),且b2=3ac,故a+c=pb.
(Ⅰ)当$p=\frac{4}{3},b=1$时,则由sinA+sinC=$\frac{4}{3}$sinB(p∈R),且b2=3ac=1,
故有a+c=$\frac{4}{3}$b=$\frac{4}{3}$,解得a=$\frac{1}{3}$,c=1; 或者a=1,c=$\frac{1}{3}$.
(Ⅱ)由余弦定理得b2=a2+c2-2accosB=(a+c)2-2ac-2accosB=p2b2-$\frac{2}{3}$b2cosB-$\frac{2}{3}{•b}^{2}$,
即p2•b2=$\frac{5}{3}{•b}^{2}$+$\frac{2}{3}{•b}^{2}$•cosB,即p2=$\frac{5}{3}$+$\frac{2}{3}$cosB,
因为角B为钝角,故-1<cosB<0,所以p2∈(1,$\frac{5}{3}$).
由题设知p∈R,又由sinA+sinC=psinB知,p是正数,
求p的取值范围为(1,$\frac{\sqrt{15}}{3}$).
点评 本题主要考查正弦定理、余弦定理的应用,钝角的余弦值的范围,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
5.若函数f(x)=cos2x+asinx在区间($\frac{π}{6}$,$\frac{π}{2}$)是减函数,则实数a∈( )
| A. | (-∞,2) | B. | (-∞,2] | C. | (4,+∞) | D. | [4,+∞) |
2.设向量$\overrightarrow{a}$=(1,2),|$\overrightarrow{b}$|=2$\sqrt{5}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°则$\overrightarrow{a}$•$\overrightarrow{b}$的值为( )
| A. | $\sqrt{5}$ | B. | 5 | C. | 5$\sqrt{5}$ | D. | 10 |
9.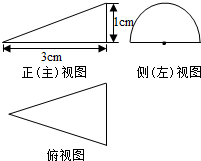 一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )
一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )
 一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )
一个几何体的三视图及其尺寸如图所示,其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的表面积是( )| A. | $\frac{(\sqrt{10}+1)π}{2}$cm2 | B. | ($\frac{(\sqrt{10}+1)π}{2}$+3)cm2 | C. | ($\frac{π}{2}$+3)cm2 | D. | ($\frac{\sqrt{10}π}{2}$+3)cm2 |
6.在长方体ABCD-A′B′C′D′中,$B{B^'}=\sqrt{3}$,B′C′=1,则AA′与BC′所成的角是( )
| A. | 90° | B. | 45° | C. | 60° | D. | 30° |