题目内容
6.在长方体ABCD-A′B′C′D′中,$B{B^'}=\sqrt{3}$,B′C′=1,则AA′与BC′所成的角是( )| A. | 90° | B. | 45° | C. | 60° | D. | 30° |
分析 由AA′∥BB′,得AA′与BC′所成的角为∠B′BC′,由此能求出AA′与BC′所成的角的大小.
解答 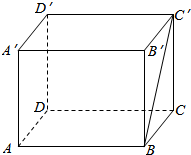 解:∵长方体ABCD-A′B′C′D′中,
解:∵长方体ABCD-A′B′C′D′中,
AA′∥BB′,
∴AA′与BC′所成的角为∠B′BC′,
∵$B{B^'}=\sqrt{3}$,B′C′=1,
∴tan∠B′BC′=$\frac{{B}^{'}{C}^{'}}{B{B}^{'}}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
∴∠B′BC=30°.
∴AA′与BC′所成的角是30°.
故选为:D.
点评 本题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知复数z=$\frac{1-i}{m+i}$为纯虚数,其中i为虚数单位,则实数m的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
14.曲线y=$\sqrt{x}$与直线y=2x-1及x轴所围成的封闭图形的面积为( )
| A. | $\frac{5}{12}$ | B. | $\frac{11}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
1.集合{x∈N|2≤x≤7}中元素的个数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
