Question

14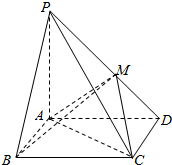．如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2，AB=1，BM⊥PD于点M．
（1）求证：AM⊥PD；
（2）求直线BM与平面ABCD所成的角的正弦值．

Answer 1

分析 （1）先证明AB垂直于PD，再根据BM垂直于PD，可得PD垂直于平面ABM，从而证得PD垂直于AM．
（2）由题意可得M是PD的中点，作MN⊥AD，N为垂足，可得∠MBN为直线BM与平面ABCD所成的角，解直角三角形BMN，求得sin∠MBN=$\frac{MN}{BM}$ 的值．

解答 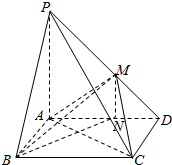（1）证明：∵PA⊥平面ABCD，AB?平面ABCD，∴PA⊥AB．
∵AB⊥AD，AD∩PA=A AD?平面PAD，PA?平面PAD，
∴AB⊥平面PAD．∵PD?平面PAD，∴AB⊥PD．
∵BM⊥PD，AB∩BM=B，AB?平面ABM，
BM?平面ABM，∴PD⊥平面ABM．
∵AM?平面ABM，∴AM⊥PD．
（2）解：由（1）知，AM⊥PD，又PA=AD，
则M是PD的中点，作MN⊥AD，N为垂足，则N为AD的中点，
MN∥PA，MN=$\frac{1}{2}$PA=1，AD⊥平面ABCD，
∠MBN为直线BM与平面ABCD所成的角．
Rt△MMB中，MN=1 BN=$\sqrt{{BA}^{2}{+AN}^{2}}$=$\sqrt{1+1}$=$\sqrt{2}$，∴BM=$\sqrt{{MN}^{2}{+BN}^{2}}$=$\sqrt{3}$，
∴sin∠MBN=$\frac{MN}{BM}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$．

点评 本题主要考查直线和平面垂直的判定和性质，直线和平面所成的角的定义和求法，属于中档题．