题目内容
17.在平行六面体ABCD-A′B′C′D′中,若$\overrightarrow{AC′}$=x$\overrightarrow{AB}$+$\frac{y}{2}$$\overrightarrow{BC}$+$\frac{z}{3}$$\overrightarrow{CC′}$,则x+y+z=6.分析 可画出图形,由图形便可得到$\overrightarrow{AC′}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC′}$,从而由空间向量基本定理便可得出x,y,z的值,从而求出x+y+z.
解答 解:如图,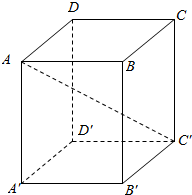
$\overrightarrow{AC′}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC′}$;
又$\overrightarrow{AC′}=x\overrightarrow{AB}+\frac{y}{2}\overrightarrow{BC}+\frac{z}{3}\overrightarrow{CC′}$;
∴由空间向量基本定理得:$\left\{\begin{array}{l}{x=1}\\{\frac{y}{2}=1}\\{\frac{z}{3}=1}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$;
∴x+y+z=6.
故答案为:6.
点评 考查向量加法的几何意义,以及空间向量基本定理.

练习册系列答案
相关题目
 已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.
已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.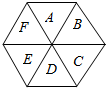 如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法?
如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法? 如图所示,已知$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>>0)点A(1,$\sqrt{2}$)是离心率为$\frac{\sqrt{2}}{2}$的椭圆C:上的一点,斜率为$\sqrt{2}$的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.
如图所示,已知$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>>0)点A(1,$\sqrt{2}$)是离心率为$\frac{\sqrt{2}}{2}$的椭圆C:上的一点,斜率为$\sqrt{2}$的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.