题目内容
若椭圆
+
=1(a>b>0)的左右焦点分别为F1,F2,线段F1F2被抛物线y2=2bx的焦点分成3:1的两段,过点C(-1,0),斜率k为的直线l交椭圆于不同两点A、B,满足
=2
.
(1)求椭圆的离心率;
(2)当三角形OAB的面积最大时,求椭圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| AC |
| CB |
(1)求椭圆的离心率;
(2)当三角形OAB的面积最大时,求椭圆的方程.
考点:椭圆的简单性质,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由c+
=3(c-
),能够求出椭圆的离心率.
(2)设直线l:x=ky-x,A(x1,y1),B(x2,y2),由
=2
,知2y2+y1=0,直线代入椭圆方程得(k2+2)y2-2ky+1-2b2=0,再利用韦达定理,结合题设条件,能够求出椭圆方程.
| b |
| 2 |
| b |
| 2 |
(2)设直线l:x=ky-x,A(x1,y1),B(x2,y2),由
| AC |
| CB |
解答:
 解:(1)由题意知,c+
解:(1)由题意知,c+
=3(c-
),…(2分)
∴b=c,
∴a2=2b2,…(3分)
∴e=
=
.…(5分)
(2)设直线l:x=ky-x,A(x1,y1),B(x2,y2),
∵
=2
,
∴(-1-x1,-y1)=2(x2+1,y2),即2y2+y1=0,①…(7分)
由(1)知,a2=2b2,∴椭圆方程为x2+2y2=2b2,
直线代入椭圆方程消去x,得(k2+2)y2-2ky+1-2b2=0,
∴y1+y2=
,…②y1y2=
,…③
由①②知,y2=-
,y1=
,…(9分)
∵S△AOB=
|y1-y2|,
∴S=3•
=3•
≤
=,…(11分)
当且仅当|k|2=2,即k=±
时取等号,
又当|k|2=2时,y1y2=-1,
∴由y1y2=
,得b2=
,
∴椭圆方程为
+
=1.…(14分)
 解:(1)由题意知,c+
解:(1)由题意知,c+| b |
| 2 |
| b |
| 2 |
∴b=c,
∴a2=2b2,…(3分)
∴e=
| c |
| a |
| ||
| 2 |
(2)设直线l:x=ky-x,A(x1,y1),B(x2,y2),
∵
| AC |
| CB |
∴(-1-x1,-y1)=2(x2+1,y2),即2y2+y1=0,①…(7分)
由(1)知,a2=2b2,∴椭圆方程为x2+2y2=2b2,
直线代入椭圆方程消去x,得(k2+2)y2-2ky+1-2b2=0,
∴y1+y2=
| 2k |
| k2+2 |
| 1-2b2 |
| k2+2 |
由①②知,y2=-
| 2k |
| k2+2 |
| 4k |
| k2+2 |
∵S△AOB=
| 1 |
| 2 |
∴S=3•
| |k| |
| k2+2 |
| 1 | ||
|
3
| ||
| 4 |
当且仅当|k|2=2,即k=±
| 2 |
又当|k|2=2时,y1y2=-1,
∴由y1y2=
| 1-2b2 |
| k2+2 |
| 5 |
| 2 |
∴椭圆方程为
| x2 |
| 5 |
| y2 | ||
|
点评:本题考查椭圆的离心率的求法,考查椭圆方程的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
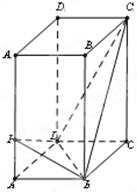 如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
 将全体正整数排成一个如图所示的三角形数阵,根据三角形数阵排列规律,数阵中第n(n≥3)行的从左至右的第3个数是
将全体正整数排成一个如图所示的三角形数阵,根据三角形数阵排列规律,数阵中第n(n≥3)行的从左至右的第3个数是