题目内容
已知如图(1),梯形ABCD中,AD∥BC,∠ABC=∠BAD=
,AB=BC=2AD=2,E、F分别是AB、CD上的动点,且EF∥BC,设AE=x(0<x<2),沿EF将梯形ABCD翻折,使使平面AEFD⊥平面EBCF,如图(2).
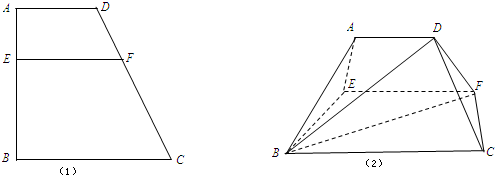
(1)求证:平面ABE⊥平面ABCD;
(2)若以B、C、D、F为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3)当f(x)取得最大值时,求二面角D-BF-C的余弦值.
| π |
| 2 |

(1)求证:平面ABE⊥平面ABCD;
(2)若以B、C、D、F为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3)当f(x)取得最大值时,求二面角D-BF-C的余弦值.
考点:用空间向量求平面间的夹角,棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由面面垂直的判定定理推出即可;
(2)由f(x)=VD-BFC=
×S△BFC×DH 求出f(x)的解析式,利用基本不等式求出其最大值;
(3)f(x)取得最大值时,EF为中位线,设D在平面EFCB上的射影为H,求出S△BHF=
•
•1=
,S△BDF=
•
•
•
=
,即可求二面角D-BF-C的余弦值.
(2)由f(x)=VD-BFC=
| 1 |
| 3 |
(3)f(x)取得最大值时,EF为中位线,设D在平面EFCB上的射影为H,求出S△BHF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
|
| ||
| 4 |
解答:
(1)证明:∵平面AEFD⊥平面EBCF,AE⊥EF,∴AE⊥平面EBCF,
∴AE⊥BC
∵BE⊥BC,AE∩BE=E,
∴BC⊥平面ABE.
又BC?平面ABCD,
∴平面ABE⊥平面ABCD. …(4分)
(2)解:∵AD∥平面BFC
∴f(x)=VD-BFC=
•
•2•(2-x)•x≤
即x=1时f(x)有最大值为
(3)解:当f(x)取得最大值时,EF为中位线,设D在平面EFCB上的射影为H,则FH=
,
∴S△BHF=
•
•1=
,
又△BDF中,BD=
=
,DF=
=
,BF=
=
,
∴cos∠BFD=
=
,
∴sin∠BFD=
,
∴S△BDF=
•
•
•
=
∴二面角D-BF-C的余弦值为
=
.
∴AE⊥BC
∵BE⊥BC,AE∩BE=E,
∴BC⊥平面ABE.
又BC?平面ABCD,
∴平面ABE⊥平面ABCD. …(4分)
(2)解:∵AD∥平面BFC
∴f(x)=VD-BFC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
即x=1时f(x)有最大值为
| 1 |
| 3 |
(3)解:当f(x)取得最大值时,EF为中位线,设D在平面EFCB上的射影为H,则FH=
| 1 |
| 2 |
∴S△BHF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
又△BDF中,BD=
| 1+1+1 |
| 3 |
1+
|
| ||
| 2 |
1+
|
| ||
| 2 |
∴cos∠BFD=
| ||||||||
2•
|
| 3 | ||
|
∴sin∠BFD=
|
∴S△BDF=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
|
| ||
| 4 |
∴二面角D-BF-C的余弦值为
| ||||
|
| ||
| 14 |
点评:本题考查求三棱锥的体积,求函数的最大值,求二面角D-BF-C的余弦值,求函数的最大值,是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD= 如图,直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别是A1B1,AB的中点,求证:
如图,直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别是A1B1,AB的中点,求证: