题目内容
设数列{an}的前n项和为Sn,满足an+1=
+n+1,n∈N*,且S4=18,令bn=
(1)求b1,b2,b3的值
(2)求数列{bn}的通项公式
(3)求证:对一切n∈N*,有
+
+…
<
.
| 3Sn |
| n |
| an |
| n |
(1)求b1,b2,b3的值
(2)求数列{bn}的通项公式
(3)求证:对一切n∈N*,有
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件利用递推思想分别求出数列{an}的前4项,由此得20a1+20=18,从而能求出b1=-
,b2=
,b3=
.
(2)由b1,b2,b3是等差数列,假设{bn}是等差数列,从而得到bn=-
+(n-1)×(
+
)=
n-
.再用数学归纳法证明,由此能求出bn=
n-
.
(3)由an=nbn=
,得
=
<
•
=
(
-
),n≥2,由此利用放缩法能证明
+
+…
<
.
| 1 |
| 10 |
| 17 |
| 20 |
| 9 |
| 5 |
(2)由b1,b2,b3是等差数列,假设{bn}是等差数列,从而得到bn=-
| 1 |
| 10 |
| 17 |
| 20 |
| 1 |
| 10 |
| 19 |
| 20 |
| 21 |
| 20 |
| 19 |
| 20 |
| 21 |
| 20 |
(3)由an=nbn=
| 19n2-21n |
| 20 |
| 1 |
| an |
| 20 |
| 19n2-21n |
| 20 |
| 19 |
| 1 |
| n(n-1) |
| 20 |
| 19 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
解答:
(1)解:∵an+1=
+n+1,n∈N*,
∴a2=3a1+2,
a3=
(a1+3a1+2)+3=6a1+6,
a4=(10a1+8)+4=10a1+12,
∵S4=18,∴20a1+20=18,解得a1=-
,
∴a2=3×(-
)+2=
,
a3=6×(-
)+6=
,
∵bn=
,
∴b1=-
,b2=
,b3=
.
(2)∵b1=-
,b2=
,b3=
.
∴b1,b2,b3是等差数列,
假设{bn}是等差数列,则bn=-
+(n-1)×(
+
)=
n-
.
再用数学归纳法证明:
①b1=
-
=-
,成立.
②假设n=k时成立,即bk=
k-
,
ak+1=
+k+1,ak=
+k,
∴3Sk-3Sk-1=3ak=kak+1-k(k+1)-(k-1)ak+k(k-1),
整理,得ak+1=2+
+ak,
将bk=
,即ak=kbk代入,得:
bk+1=
=
=
(k+1)-
,
∴bn=
n-
.
(3)证明:∵an=nbn=
,
∴
=
<
•
=
(
-
),n≥2,
∴
+
+…
<
+
(1-
+
-
+…+
-
)
=-10+
(1-
)<
.
∴
+
+…
<
.
| 3Sn |
| n |
∴a2=3a1+2,
a3=
| 3 |
| 2 |
a4=(10a1+8)+4=10a1+12,
∵S4=18,∴20a1+20=18,解得a1=-
| 1 |
| 10 |
∴a2=3×(-
| 1 |
| 10 |
| 17 |
| 10 |
a3=6×(-
| 1 |
| 10 |
| 27 |
| 5 |
∵bn=
| an |
| n |
∴b1=-
| 1 |
| 10 |
| 17 |
| 20 |
| 9 |
| 5 |
(2)∵b1=-
| 1 |
| 10 |
| 17 |
| 20 |
| 9 |
| 5 |
∴b1,b2,b3是等差数列,
假设{bn}是等差数列,则bn=-
| 1 |
| 10 |
| 17 |
| 20 |
| 1 |
| 10 |
| 19 |
| 20 |
| 21 |
| 20 |
再用数学归纳法证明:
①b1=
| 19 |
| 20 |
| 21 |
| 20 |
| 1 |
| 10 |
②假设n=k时成立,即bk=
| 19 |
| 20 |
| 21 |
| 20 |
ak+1=
| 3Sk |
| k |
| 3Sk-1 |
| k-1 |
∴3Sk-3Sk-1=3ak=kak+1-k(k+1)-(k-1)ak+k(k-1),
整理,得ak+1=2+
| 2ak |
| k |
将bk=
| ak |
| k |
bk+1=
| 2+2bk+kbk |
| k+1 |
=
| 19k2+17k-2 |
| 20(k+1) |
=
| 19 |
| 20 |
| 21 |
| 20 |
∴bn=
| 19 |
| 20 |
| 21 |
| 20 |
(3)证明:∵an=nbn=
| 19n2-21n |
| 20 |
∴
| 1 |
| an |
| 20 |
| 19n2-21n |
| 20 |
| 19 |
| 1 |
| n(n-1) |
| 20 |
| 19 |
| 1 |
| n-1 |
| 1 |
| n |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| a1 |
| 20 |
| 19 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
=-10+
| 20 |
| 19 |
| 1 |
| n |
| 1 |
| 2 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
点评:本题考查数列的前3项及通项公式的求法,考查不等式的证明,解题时要认真审题,注意放缩法的合理运用.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
已知a、b∈R,直线l1:ax+2y+3=0和直线l2:x+by+2=0,则“ab=2”是“l1∥l2”的( )
| A、充分不必要条件. |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件. |
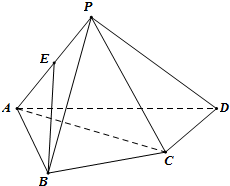 在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)
在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)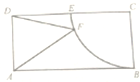 如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是
如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是
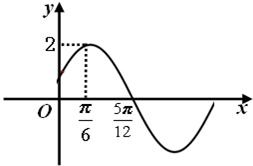 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<