题目内容
某民营企业每年度清理排污费用24万元,为了环保和节省开支,决定安排一个可使用15年的排污设备,安装设备的费用(万元)与设备容量(kw)成正比例,比例系数为0.5,安装设备后企业每年治污的费用w(万元)与该设备容量x(kw)之间的函数关系式是w(x)=
(k为常数,x≥0),设F(万元)为该企业安装设备的费用与15年所有治污费用的和.
(1)求k的值,并写出与x的关系式;
(2)当x为何值时,F有最小值?并求出最小值是多少?
| k |
| 20x+100 |
(1)求k的值,并写出与x的关系式;
(2)当x为何值时,F有最小值?并求出最小值是多少?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用,不等式的解法及应用
分析:(1)C(0)的实际意义是安装这种太阳能电池板的面积为0时的用电费用,依题意,C(0)=
=24,可求得k,从而得到F关于x的函数关系式;
(2)利用基本不等式即可求得F取得的最小值及F取得最小值时x的值.
| k |
| 100 |
(2)利用基本不等式即可求得F取得的最小值及F取得最小值时x的值.
解答:
解:(1)C(0)的实际意义是安装这种太阳能电池板的面积为0时的用电费用,
即未安装电阳能供电设备时全村每年消耗的电费…(2分)
由C(0)=
=24,得k=2400 …(3分)
所以F=15×
+0.5x=
+0.5x,x≥0…(7分)
(2)因为
+0.5(x+5)-2.5≥2
-2.5=57.5,…(10分)
当且仅当
=0.5(x+5),即x=55时取等号 …(13分)
所以当x为55平方米时,F取得最小值为57.5万元…(14分)
即未安装电阳能供电设备时全村每年消耗的电费…(2分)
由C(0)=
| k |
| 100 |
所以F=15×
| 2400 |
| 20x+100 |
| 1800 |
| x+5 |
(2)因为
| 1800 |
| x+5 |
| 1800×0.5 |
当且仅当
| 1800 |
| x+5 |
所以当x为55平方米时,F取得最小值为57.5万元…(14分)
点评:本题考查函数最值的应用,着重考查分析与理解能力,考查基本不等式的应用,属于中档题.

练习册系列答案
相关题目
有3位同学参加测试,假设每位同学能通过测试的概率都是
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
=(2,y,2),
=(x,-1,1),若
⊥
,则实数x,y满足的关系式为( )
| a |
| b |
| a |
| b |
| A、2x-y=0 |
| B、2x+y=0 |
| C、2x+y-2=0 |
| D、2x-y+2=0 |
二项式(2x+
)6的展开式中,常数项的值是( )
| 1 |
| x2 |
| A、240 | B、60 |
| C、192 | D、180 |
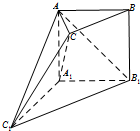 如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.
如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.