Question

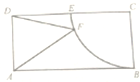如图，矩形ABCD中，AB=2，BC=1，以点C为圆心，CB为半径的圆与边DC交于点E，F是

BE

上任意一点（包括端点），在矩形ABCD内随机取一点M，则点M落在△AFD内部的概率的取值范围是

 

．

Answer 1

考点：几何概型

专题：概率与统计

分析：根据几何概型的公式，只要求出△AFD的面积范围，由几何概型的概率公式可求点M落在△AFD内部的概率的取值范围

解答： 解：由题意，设△AFD的高为h，因为F是

BE

上任意一点（包括端点），所以h∈[1，2]，所以△AFD的面积范围为[

1

2

，1]，又矩形ABCD的面积为2，
由几何概型的公式可得
点M落在△AFD内部的概率的取值范围[

1

4

，

1

2

]；
故答案为：[

1

4

，

1

2

]．

点评：本题考查了几何概型的概率公式的运用，关键是求出△AFD的面积范围．