题目内容
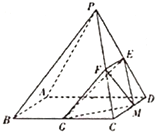 如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.(1)求证:直线EG∥平面PAB;
(2)若平面PAD⊥平面ABCD,M是线段CD上任一点,求三棱锥M-EFG的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)取PA的中点N,连接EN,BN,证明四边形ENBG为平行四边形,可得EG∥BN,从而证明直线EG∥平面PAB;
(2)CD上的点M到平面EFG的距离等于D到平面EFG的距离,可得VM-EFG=VD-EFG.
(2)CD上的点M到平面EFG的距离等于D到平面EFG的距离,可得VM-EFG=VD-EFG.
解答:
 (1)证明:取PA的中点N,连接EN,BN,则
(1)证明:取PA的中点N,连接EN,BN,则
∵E,N为PD,PA的中点,
∴EN∥AD,EN=
AD,
∵BG∥AD,BG=
AD,
∴BG∥EN,BG=EN,
∴四边形ENBG为平行四边形,
∴EG∥BN,EG=BN,
∵BN?平面PAB,EG?平面PAB,
∴直线EG∥平面PAB;
(2)解:∵CD∥EF,∴CD∥平面EFG,
故CD上的点M到平面EFG的距离等于D到平面EFG的距离,∴VM-EFG=VD-EFG,
取AD的中点H,连接EH,HG,则EF∥GH,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊥AD,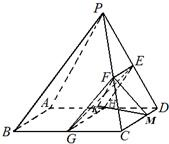
∴CD⊥平面PAD,
∵EF∥CD,EF⊥平面PAD,EH?平面PAD,
∴EF⊥EH,
∴S△EFG=S△EFH=
EF•EH=2
∵平面EFGH⊥平面PBD,平面EFGH∩平面PBD=EH,
∴D到平面EFG的距离即三角形EHD的高,等于
∴VM-EFG=VD-EFG=
 (1)证明:取PA的中点N,连接EN,BN,则
(1)证明:取PA的中点N,连接EN,BN,则∵E,N为PD,PA的中点,
∴EN∥AD,EN=
| 1 |
| 2 |
∵BG∥AD,BG=
| 1 |
| 2 |
∴BG∥EN,BG=EN,
∴四边形ENBG为平行四边形,
∴EG∥BN,EG=BN,
∵BN?平面PAB,EG?平面PAB,
∴直线EG∥平面PAB;
(2)解:∵CD∥EF,∴CD∥平面EFG,
故CD上的点M到平面EFG的距离等于D到平面EFG的距离,∴VM-EFG=VD-EFG,
取AD的中点H,连接EH,HG,则EF∥GH,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊥AD,

∴CD⊥平面PAD,
∵EF∥CD,EF⊥平面PAD,EH?平面PAD,
∴EF⊥EH,
∴S△EFG=S△EFH=
| 1 |
| 2 |
∵平面EFGH⊥平面PBD,平面EFGH∩平面PBD=EH,
∴D到平面EFG的距离即三角形EHD的高,等于
| 3 |
∴VM-EFG=VD-EFG=
2
| ||
| 3 |
点评:此题考查直线与平面平行的判断及三棱锥M-EFG的体积,考查学生分析解决问题的能力,正确运用线与平面平行的判断是关键.

练习册系列答案
相关题目
若方程
+
=1表示的图形是双曲线,则k的取值范围为( )
| x2 |
| 2-k |
| y2 |
| k-1 |
| A、k>2或k<1 |
| B、1<k<2 |
| C、-2<k<1 |
| D、-1<k<2 |
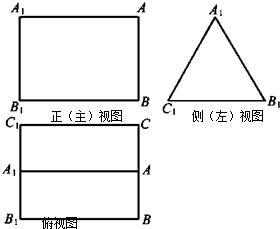 如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.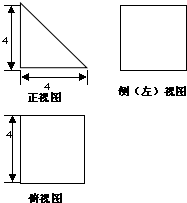 如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.
如图为某几何体的三视图,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,求该几何体的表面积.