题目内容
设的△ABC的内角A,B,C所对的边分别为a,b,c,已知a=1,b=2,cosC=
.
(1)求c的值;
(2)求cos(A-C)的值.
| 1 |
| 4 |
(1)求c的值;
(2)求cos(A-C)的值.
考点:余弦定理,两角和与差的余弦函数
专题:解三角形
分析:(1)利用余弦定理列出关系式,将a,b,cosC的值代入即可求出c的值;
(2)由cosC的值求出sinC的值,由正弦定理列出关系式,将a,c,sinC的值代入求出sinA的值,进而求出cosA的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
(2)由cosC的值求出sinC的值,由正弦定理列出关系式,将a,c,sinC的值代入求出sinA的值,进而求出cosA的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答:
解:(1)∵△ABC中,a=1,b=2,cosC=
,
∴由余弦定理得:c2=a2+b2-2abcosC=1+4-1=4,
则c=2;
(2)∵cosC=
,
∴sinC=
=
,
∵a=1,b=c=2,
∴由正弦定理
=
得:
=
,
解得:sinA=
,
∵a<b,∴A<B,即A为锐角,
∴cosA=
=
,
则cos(A-C)=cosAcosC+sinAsinC=
×
+
×
=
.
| 1 |
| 4 |
∴由余弦定理得:c2=a2+b2-2abcosC=1+4-1=4,
则c=2;
(2)∵cosC=
| 1 |
| 4 |
∴sinC=
| 1-cos2C |
| ||
| 4 |
∵a=1,b=c=2,
∴由正弦定理
| a |
| sinA |
| c |
| sinC |
| 1 |
| sinA |
| 2 | ||||
|
解得:sinA=
| ||
| 8 |
∵a<b,∴A<B,即A为锐角,
∴cosA=
| 1-sin2A |
| 7 |
| 8 |
则cos(A-C)=cosAcosC+sinAsinC=
| 7 |
| 8 |
| 1 |
| 4 |
| ||
| 8 |
| ||
| 4 |
| 11 |
| 16 |
点评:此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
某人连续射击8次,命中4次且恰好有3次连在一起的结果有( )
| A、12种 | B、6种 |
| C、20种 | D、10种 |
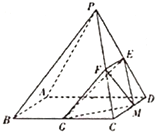 如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.