题目内容
已知矩阵A=
(k≠0)的一个特征向量为
=
,矩阵A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1).
(1)求实数a,k的值;
(2)求直线x+2y+1=0在矩阵A的对应变换下得到的图形方程.
|
| a |
|
(1)求实数a,k的值;
(2)求直线x+2y+1=0在矩阵A的对应变换下得到的图形方程.
考点:特征值、特征向量的应用
专题:
分析:(1)利用特征值与特征向量的定义,可求a;利用A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1),可求k的值.
(2)利用矩阵变换,确定坐标之间的关系,即可得到在A对应的变换作用下的新曲线的方程.
(2)利用矩阵变换,确定坐标之间的关系,即可得到在A对应的变换作用下的新曲线的方程.
解答:
解:设特征向量为
=
,对应的特征值为λ,则
=λ
,即
因为k≠0,所以a=2.
因为A-1
=
,所以A
=
,所以2+k=3,解得k=1.
综上,a=2,k=1.
(2)设直线x+2y+1=0上任一点P(x,y)在A对应的变换作用下对应点P'(x',y'),
∴
=
,
∴
,
代入x+2y+1=0,化简可得x′+3y′+2=0,
∴得到的图形方程为x+3y+2=0.
| a |
|
|
|
|
|
因为A-1
|
|
|
|
综上,a=2,k=1.
(2)设直线x+2y+1=0上任一点P(x,y)在A对应的变换作用下对应点P'(x',y'),
∴
|
|
|
∴
|
代入x+2y+1=0,化简可得x′+3y′+2=0,
∴得到的图形方程为x+3y+2=0.
点评:本题考查矩阵的乘法,矩阵变换,以及特征值与特征向量的计算,确定坐标之间的关系是关键.

练习册系列答案
相关题目
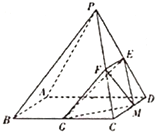 如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.