题目内容
设函数f(x)=2x3-12x.
(1)求函数f(x)的单调递增区间.
(2)求函数f(x)在[-1,3]上的最大值和最小值.
(1)求函数f(x)的单调递增区间.
(2)求函数f(x)在[-1,3]上的最大值和最小值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(1)由f′(x)=6x2-12,令f′(x)>0,从而可求f(x)的单调递增区间.
(2)由(1)得:f(x)在[-1,
)递减,在(
,3]递增,而f(-1)=10,f(
)=-8
,f(3)=18,从而f(x)在[-1,3]上的最大值是18,最小值是-8
.
(2)由(1)得:f(x)在[-1,
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:
解(1)∵f(x)=2x3-12x.
∴f′(x)=6x2-12,
令f′(x)>0,解得:x>
,x<-
,
∴f(x)的单调递增区间是(-∞,-
)和(
,+∞).
(2)由(1)得:
f(x)在[-1,
)递减,在(
,3]递增,
∴x=
是极小值点,
而f(-1)=10,f(
)=-8
,f(3)=18,
∴f(x)在[-1,3]上的最大值是18,最小值是-8
.
∴f′(x)=6x2-12,
令f′(x)>0,解得:x>
| 2 |
| 2 |
∴f(x)的单调递增区间是(-∞,-
| 2 |
| 2 |
(2)由(1)得:
f(x)在[-1,
| 2 |
| 2 |
∴x=
| 2 |
而f(-1)=10,f(
| 2 |
| 2 |
∴f(x)在[-1,3]上的最大值是18,最小值是-8
| 2 |
点评:本题考察了函数的单调性,函数在闭区间上的最值问题,导数的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
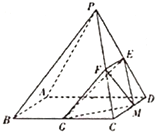 如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.