Question

已知双曲线x²-

y2

3

=1．
（1）若椭圆C与该双曲线共焦点，且有一交点p（2，3），求椭圆C方程；
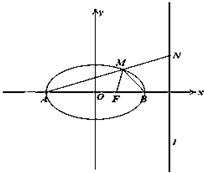
（2）设（1）中椭圆C的左、右顶点分别为A，B，右焦点为F，直线l为椭圆C的右准线，N为l上的一动点，且在x轴上方，直线AN与椭圆交于点M．
①若AM=MN，求∠AMB的余弦值；
②设过A，F，N三点的圆与y轴交于P、Q两点，当线段PQ的中点为（0，9）时，求这个圆的方程．

Answer 1

考点：圆锥曲线的综合

专题：圆锥曲线的定义、性质与方程

分析：（1）设出椭圆方程，利用椭圆C与该双曲线共焦点，且有一交点P（2，3），建立方程组，求出几何量，即可得出椭圆的标准方程；
（2）①先求出M的坐标，再利用向量的数量积公式，即可求∠AMB的余弦值；
②设过A，F，N三点的圆的方程，代入点的坐标，利用圆与y轴交于P、Q两点，线段PQ的中点为（0，9），结合韦达定理，即可求这个圆的方程．

解答： 解：（1）由题意，设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，
∵双曲线焦点为（±2，0），椭圆C与该双曲线共焦点，且有一交点P（2，3），
∴

a2-b2=4 4 a2 + 9 b2 =1

，∴a²=16，b²=12．
故椭圆方程为

x2

16

+

y2

12

=1．
（2）①由已知，A（-4，0），B（4，0），F（2，0），直线l的方程为x=8．
设N（8，t）（t＞0），则
∵AM=MN，∴M（2，

t

2

）
由点M在椭圆上，得t=6，故所求的点M的坐标为M（2，3）．
∴

MA

=（-6，-3），

MB

=（2，-3），∴cos∠AMB=

MA • MB

| MA || MB |

=

-12+9

36+9 • 4+9

=-

65

65

．
②设圆的方程为x²+y²+Dx+Ey+F=0，将A、F、N三点坐标代入，得

16-4D+F=0 4+2D+F=0 64+t2+8D+Et+F=0

，
∴D=2，E=-t-

72

t

，F=-8，
∴圆的方程为x2+y2+2x-(t+

72

t

)y-8=0，令x=0，得y2-(t+

72

t

)y-8=0，
设P（0，y₁），Q（0，y₂），则y1+y2=t+

72

t

，
∵线段PQ的中点为（0，9），
∴t+

72

t

=18，
∴圆的方程为x²+y²+2x-18y-8=0．

点评：本题考查椭圆的方程，考查圆的方程，考查向量知识的应用，考查韦达定理，考查学生的计算能力，属于中档题．