题目内容
已知
=(1,5,-2),
=(m,2,m+2),若
⊥
,则m的值为 .
| a |
| b |
| a |
| b |
考点:数量积判断两个平面向量的垂直关系
专题:空间向量及应用
分析:根据向量垂直于向量数量积之间的关系解方程即可.
解答:
解:∵
⊥
,
∴
•
=0,
即(1,5,-2)•(m,2,m+2)=0,
∴m+10-2m-4=0,
解得m=6.
故答案为:6.
| a |
| b |
∴
| a |
| b |
即(1,5,-2)•(m,2,m+2)=0,
∴m+10-2m-4=0,
解得m=6.
故答案为:6.
点评:本题主要考查空间向量数量积的应用,利用向量垂直转化为向量数量积等于0是解决本题的关键,比较基础.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
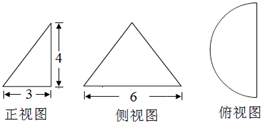 某几何体的三视图如图所示(单位:cm),则其体积和表面积分别是( )
某几何体的三视图如图所示(单位:cm),则其体积和表面积分别是( )| A、6πcm3和12(1+π)cm2 |
| B、6πcm3和12πcm2 |
| C、12πcm3和12(1+π)cm2 |
| D、12πcm3和12πcm2 |
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A、y=-ln|x| |
| B、y=x3 |
| C、y=2|x| |
| D、y=cosx |
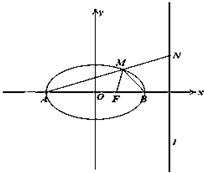 已知双曲线x2
已知双曲线x2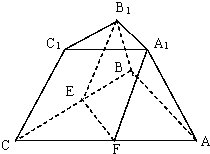 在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.
在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.