题目内容
已知函数f(x)=ex+ae-x是R上的奇函数,
(1)求a的值;
(2)试判断函数f(x)的单调性,并证明你的结论.
(1)求a的值;
(2)试判断函数f(x)的单调性,并证明你的结论.
考点:函数奇偶性的性质,函数单调性的性质
专题:函数的性质及应用
分析:(1)根据函数f(x)=ex+ae-x是R上的奇函数,可得f(0)=1+a=0,从而求得a的值.
(2)由(1)可得函数f(x)的解析式,再根据增函数减去减函数的差为增函数,可得函数f(x)在R上是增函数.
(2)由(1)可得函数f(x)的解析式,再根据增函数减去减函数的差为增函数,可得函数f(x)在R上是增函数.
解答:
解:(1)∵函数f(x)=ex+ae-x是R上的奇函数,∴f(0)=1+a=0,∴a=-1.
(2)由(1)可得函数f(x)=ex-
,再根据y=ex在R上是增函数,且y=
在R上是减函数,
可得函数f(x)=ex-
在R上是增函数.
(2)由(1)可得函数f(x)=ex-
| 1 |
| ex |
| 1 |
| ex |
可得函数f(x)=ex-
| 1 |
| ex |
点评:本题主要考查函数的奇偶性的应用,注意利用增函数减去减函数,结果为增函数,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若集合A={x∈R|y=lg(2-x)},B={y∈R|y=2x-1,x∈A},则∁R(A∩B)=( )
| A、R |
| B、(-∞,0]∪[2,+∞) |
| C、[2,+∞) |
| D、(-∞,0] |
定义在R上的偶函数f(x)满足f(x)=-
且f(4)=-2,则f(2018)的值为( )
| 1 |
| f(x+3) |
| A、4 | ||
| B、-2 | ||
| C、2 | ||
D、
|
 已知双曲线x2
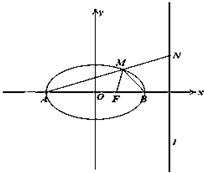
已知双曲线x2 如图,已知椭圆
如图,已知椭圆