题目内容
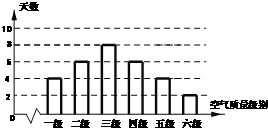 根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQI(为整数)的不同,可将空气质量分级如下表:| AQI(数值) | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
(1)估计该城市本月(按30天计)空气质量类别为中度污染的概率;
(2)在空气质量类别颜色为紫色和褐红色的数据中任取2个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
考点:等可能事件的概率,频率分布直方图
专题:概率与统计
分析:(1)根据表格和条形统计图可得空气质量类别为中度污染的天数,然后利用古典概型的概率公式可求出所求;
(2)由条形图知,空气质量类别颜色为紫色的数据有4个,分别设为a、b、c、d,空气质量类别颜色为褐红色的数据有2个,分别设为e、f,然后列举出基本事件,以及至少有一个数据反映的空气质量类别颜色为褐红色的事件,最后根据古典概型的概率公式解之即可.
(2)由条形图知,空气质量类别颜色为紫色的数据有4个,分别设为a、b、c、d,空气质量类别颜色为褐红色的数据有2个,分别设为e、f,然后列举出基本事件,以及至少有一个数据反映的空气质量类别颜色为褐红色的事件,最后根据古典概型的概率公式解之即可.
解答:
解:(1)由条形统计图可知,空气质量类别为中度污染的天数为6,
所以该城市本月内空气质量类别为中度污染的概率 P=
=
.
(2)由条形图知,空气质量类别颜色为紫色的数据有4个,分别设为a、b、c、d,空气质量类别颜色为褐红色的数据有2个,分别设为e、f.
设从以上6个数据任取2个,至少有一个数据反映的空气质量类别颜色为褐红色为事件A,
则基本事件有:(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f),(e,f)共15种可能,
A包含的基本事件有:(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f),(e,f)9种可能,
故所求的概率P(A)=
=
.
所以该城市本月内空气质量类别为中度污染的概率 P=
| 6 |
| 30 |
| 1 |
| 5 |
(2)由条形图知,空气质量类别颜色为紫色的数据有4个,分别设为a、b、c、d,空气质量类别颜色为褐红色的数据有2个,分别设为e、f.
设从以上6个数据任取2个,至少有一个数据反映的空气质量类别颜色为褐红色为事件A,
则基本事件有:(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f),(e,f)共15种可能,
A包含的基本事件有:(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f),(e,f)9种可能,
故所求的概率P(A)=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题主要考查条形图,以及古典概型的概率计算,常用利用列举法进行求解,同时考查学生的阅读能力和分析问题的能力,属于基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
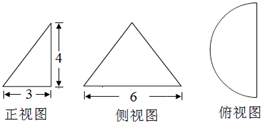 某几何体的三视图如图所示(单位:cm),则其体积和表面积分别是( )
某几何体的三视图如图所示(单位:cm),则其体积和表面积分别是( )| A、6πcm3和12(1+π)cm2 |
| B、6πcm3和12πcm2 |
| C、12πcm3和12(1+π)cm2 |
| D、12πcm3和12πcm2 |
若直线y=x+m与圆x2+y2+4x+2=0有两个不同的公共点,则实数m的取值范围是( )
| A、(0,4) | ||||
| B、(-4,0) | ||||
C、(-2-
| ||||
D、(2-
|
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A、y=-ln|x| |
| B、y=x3 |
| C、y=2|x| |
| D、y=cosx |
 (坐标系与参数方程选做题)如图所示的极坐标系中,以M(4,
(坐标系与参数方程选做题)如图所示的极坐标系中,以M(4,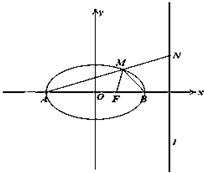 已知双曲线x2
已知双曲线x2