题目内容
一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…
若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前200个圈中的●的个数是 .
若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前200个圈中的●的个数是
考点:归纳推理
专题:规律型
分析:根据黑点和圈的排列规律,即可确定前200个圈中的●的个数.
解答:
解:根据把这些圈个数看作是数列:1,1,2,1,3,1,4,1…,
前n项和小于等于200时的最大的整数项数解:s=(1+2+3+…+n)+n=
+n=
≤200
∴n(n+3)≤400
∴n=17时,17×20=340,
当n=18时,18×21=378,
当n=19时,19×22=418>400,
∴n=18.
故答案为:18.
前n项和小于等于200时的最大的整数项数解:s=(1+2+3+…+n)+n=
| n(n+1) |
| 2 |
| n(n+3) |
| 2 |
∴n(n+3)≤400
∴n=17时,17×20=340,
当n=18时,18×21=378,
当n=19时,19×22=418>400,
∴n=18.
故答案为:18.
点评:本题主要考查归纳推理的应用,利用数列求和的知识是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A、y=-ln|x| |
| B、y=x3 |
| C、y=2|x| |
| D、y=cosx |
定义在R上的偶函数f(x)满足f(x)=-
且f(4)=-2,则f(2018)的值为( )
| 1 |
| f(x+3) |
| A、4 | ||
| B、-2 | ||
| C、2 | ||
D、
|
在空间直角坐标系中,点P(-2,4,4)关于x轴和坐标原点的对称点分别为P1和P2,则|P1P2|=( )
| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
 已知双曲线x2
已知双曲线x2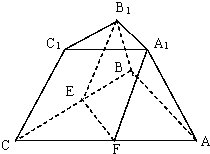 在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.
在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.