题目内容
在数列{an}中,前n项和为Sn,且Sn=
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
,数列{bn}前n项和为Tn,比较Tn与2的大小.
| n(n+1) |
| 2 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| an |
| 2n |
考点:数列的求和,不等式比较大小,数列的函数特性
专题:计算题,等差数列与等比数列
分析:(Ⅰ)当n=1时,a1=S1=1;当n≥2时,an=Sn-Sn-1=n,经验证,a1=1满足上式,于是可求得数列{an}的通项公式;
(Ⅱ)依题意知,bn=
=
,利用错位相减法即可求得数列{bn}前n项和为Tn,从而可与2比较大小.
(Ⅱ)依题意知,bn=
| an |
| 2n |
| n |
| 2n |
解答:
解:(Ⅰ)当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=
-
=n,
经验证,a1=1满足上式.
∴数列{an}的通项公式an=n.(6分)
(Ⅱ)∵bn=
=
,
∴Tn=
+
+
+…+
,
则
Tn=
+
+
+…+
,
两式相减,得
Tn=
+
+
+…+
-
=
-
=1-
-
,
∴Tn=2-
<2.
当n≥2时,an=Sn-Sn-1=
| n(n+1) |
| 2 |
| (n-1)n |
| 2 |
经验证,a1=1满足上式.
∴数列{an}的通项公式an=n.(6分)
(Ⅱ)∵bn=
| an |
| 2n |
| n |
| 2n |
∴Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
则
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
两式相减,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
=
| ||||
1-
|
| n |
| 2n+1 |
=1-
| 1 |
| 2n |
| n |
| 2n+1 |
∴Tn=2-
| n+2 |
| 2n |
点评:本题考查数列的求和,着重考查错位相减法求和,考查不等式比较大小,属于中档题.

练习册系列答案
相关题目
已知点P(x,y)满足x2+y2-2y=0,则u=
的取值范围是( )
| y+1 |
| x |
A、-
| ||||||||
B、μ≤-
| ||||||||
C、-
| ||||||||
D、μ≤-
|
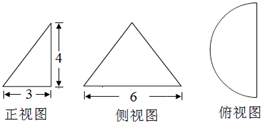 某几何体的三视图如图所示(单位:cm),则其体积和表面积分别是( )
某几何体的三视图如图所示(单位:cm),则其体积和表面积分别是( )| A、6πcm3和12(1+π)cm2 |
| B、6πcm3和12πcm2 |
| C、12πcm3和12(1+π)cm2 |
| D、12πcm3和12πcm2 |
 (坐标系与参数方程选做题)如图所示的极坐标系中,以M(4,
(坐标系与参数方程选做题)如图所示的极坐标系中,以M(4,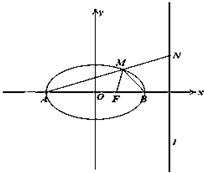 已知双曲线x2
已知双曲线x2