题目内容
14.已知直线l1:x+2y-1=0与直线l2:mx-y=0垂直,则m=( )| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 由两条直线互相垂直的条件,建立关于m的方程,解之即可得到实数m的值.
解答 解:∵直线l1:x+2y-1=0与直线l2:mx-y=0互相垂直
∴可得m-2=0,解之得m=2,
故选:A.
点评 本题给出含有字母参数m的直线方程,在它们相互垂直的情况下求参数m的值.着重考查了两条直线相互垂直的充要条件,属于基础题.

练习册系列答案
相关题目
5.已知$A(3,0),B(0,3),C(cosα,sinα),\overrightarrow{AC}⊥\overrightarrow{BC}$,则sin2α的值为( )
| A. | $\frac{8}{9}$ | B. | $-\frac{8}{9}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
2.已知函数$f(x)=\left\{\begin{array}{l}-{x^2}-2x+3(x≤1)\\ 1nx(x>1)\end{array}\right.$,若关于x的方程$f(x)=kx-\frac{1}{2}$恰有四个不相等的实数根,则实数k的取值范围是( )
| A. | $({\frac{1}{2},\sqrt{e}})$ | B. | $[{\frac{1}{2},\sqrt{e}})$ | C. | $({\frac{1}{2},\frac{{\sqrt{e}}}{e}}]$ | D. | $({\frac{1}{2},\frac{{\sqrt{e}}}{e}})$ |
19.已知实数a,b,c满足 ${(\frac{1}{3})^x}=2,{log_3}b=\frac{1}{2},{c^{-3}}=2$,则实数a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
3.已知Sn为数列{an}的前n项和且Sn=2an-2,则S5-S4的值为( )
| A. | 8 | B. | 10 | C. | 16 | D. | 32 |
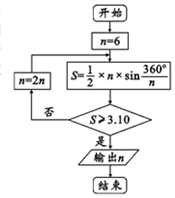 公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )
公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )