题目内容
5.已知$A(3,0),B(0,3),C(cosα,sinα),\overrightarrow{AC}⊥\overrightarrow{BC}$,则sin2α的值为( )| A. | $\frac{8}{9}$ | B. | $-\frac{8}{9}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
分析 利用两个向量垂直的性质可得$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,再利用两个向量数量积公式求得sinα+cosα的值,再平方,可得sin2α的值.
解答 解:∵已知$A(3,0),B(0,3),C(cosα,sinα),\overrightarrow{AC}⊥\overrightarrow{BC}$,
∴$\overrightarrow{AC}$•$\overrightarrow{BC}$=(cosα-3,sinα)•(cosα,sinα-3)=(cosα-3)cosα+sinα(sinα-3)
=1-3(sinα+cosα)=0,∴sinα+cosα=$\frac{1}{3}$,平方可得1+2sinαcosα=$\frac{1}{9}$,
∴2sinαcosα=sin2α=-$\frac{8}{9}$,
故选:B.
点评 本题主要考查两个向量垂直的性质,两个向量坐标形式的运算,两个向量数量积公式,二倍角公式的应用,属于中档题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
13.已知数列{an}满足${a_{n+1}}=\sqrt{{a_n}^2-2{a_n}+2}+1(n∈{N_+})$,则使不等式a2016>2017成立的所有正整数a1的集合为( )
| A. | {a1|a1≥2017,a1∈N+} | B. | {a1|a1≥2016,a1∈N+} | C. | {a1|a1≥2015,a1∈N+} | D. | {a1|a1≥2014,a1∈N+} |
17.若复数z满足z(4-i)=5+3i(i为虚数单位),则复数z的共轭复数为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
14.已知直线l1:x+2y-1=0与直线l2:mx-y=0垂直,则m=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.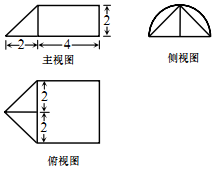 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$+8π | B. | $\frac{16}{3}$+8π | C. | $\frac{8}{3}$+16π | D. | $\frac{16}{3}$+16π |
 已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.
已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.