题目内容
6.已知直线l1:y=k(x+1)+2,(k∈R)过定点P.(1)求定点P的坐标;
(2)若直线l1与直线l2:3x-(k-2)y+5=0平行,求k的值并求此时两直线间的距离.
分析 (1)直线l1:y=k(x+1)+2,可得$\left\{\begin{array}{l}{x+1=0}\\{y=2}\end{array}\right.$,即可求定点P的坐标;
(2)利用两条直线平行的条件,求出k,利用两直线间的距离公式可得结论.
解答 解:(1)直线l1:y=k(x+1)+2,可得$\left\{\begin{array}{l}{x+1=0}\\{y=2}\end{array}\right.$,∴x=-1,y=2,∴P(-1,2);
(2)直线l1与直线l2:3x-(k-2)y+5=0平行,则$\frac{3}{k-2}$=k,解得k=-1或3,
k=3时,两条直线重合;
k=-1时,直线l1:3x+3y-3=0,直线l2:3x+3y+5=0,两直线间的距离d=$\frac{|5+3|}{\sqrt{9+9}}$=$\frac{4\sqrt{2}}{3}$.
点评 本题考查直线过定点,考查两条直线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
17.若复数z满足z(4-i)=5+3i(i为虚数单位),则复数z的共轭复数为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
14.已知直线l1:x+2y-1=0与直线l2:mx-y=0垂直,则m=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
1. 如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )
如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )
 如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )
如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
11.命题“?x∈R,都有x2≥0”的否定为( )
| A. | 不存在x0∈R,使得$x_0^2<0$ | B. | ?x∈R,都有x2<0 | ||
| C. | ?x0∈R,使得$x_0^2≥0$ | D. | ?x0∈R,使得$x_0^2<0$ |
15.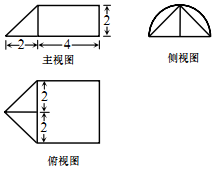 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$+8π | B. | $\frac{16}{3}$+8π | C. | $\frac{8}{3}$+16π | D. | $\frac{16}{3}$+16π |
