题目内容
2.已知函数f(x)=log2(x2-2x-3),则f(x)的定义域为{x|x>3或x<-1},它的单调递增区间是(3,+∞).分析 根据对数函数的真数大于0,可得定义域;根据复合函数的单调性,即可求解函数f(x)的单调递增区间.
解答 解:函数f(x)=log2(x2-2x-3),
其定义域满足:x2-2x-3>0,
解得:x>3或x<-1
∴f(x)的定义域为{x|x>3或x<-1};
∵f(x)=log2u是单调递增,
∴只需求u=x2-2x-3的单调增区间即可.
其对称轴x=1,开口向上,定义域为{x|x>3或x<-1};
∴函数u在(3,+∞)单调递增
根据复合函数的单调性“同增异减”可得函数f(x)的单调增区间为(3,+∞)
故答案为:{x|x>3或x<-1};(3,+∞).
点评 本题考查了对数函数的性质和复合函数的单调性的判断及运用.属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
14.已知直线l1:x+2y-1=0与直线l2:mx-y=0垂直,则m=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.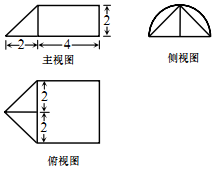 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$+8π | B. | $\frac{16}{3}$+8π | C. | $\frac{8}{3}$+16π | D. | $\frac{16}{3}$+16π |
19.执行如图所示的程序框图,则输出S的值是( )
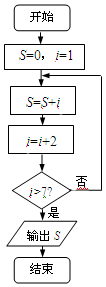

| A. | 9 | B. | 16 | C. | 25 | D. | 27 |
11.若函数f(x)=$\frac{sinx+a}{cosx}$在区间(0,$\frac{π}{2}$)上单调递增,则实数a的取值范围是( )
| A. | a≤-1 | B. | a≤2 | C. | a≥-1 | D. | a≤1 |
12.若sin(π-α)=$\frac{1}{3}$,且$\frac{π}{2}$≤α≤π,则cosα=( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
