题目内容
在一次人才招聘会上,有A,B,C三种不同的技工面向社会招聘,已知某技术人员应聘A,B,C三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
(1)求该技术人员被录用的概率;
(2)设ξ表示该技术人员被录用的工种数与未被录用的工种数的乘积,求ξ的分布列和数学期望.
(1)求该技术人员被录用的概率;
(2)设ξ表示该技术人员被录用的工种数与未被录用的工种数的乘积,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)利用对立事件求出被录用的概率;
(2)设ξ表示该技术人员被录用的工种数与未被录用的工种数的乘积,求出ξ的可能取值,再求出ξ的分布列与数学期望.
(2)设ξ表示该技术人员被录用的工种数与未被录用的工种数的乘积,求出ξ的可能取值,再求出ξ的分布列与数学期望.
解答:
解:(1)该技术人员被录用的概率是
P=1-(1-0.8)×(1-0.5)×(1-0.2)=1-0.2×0.5×0.8=0.92;
(2)设ξ表示该技术人员被录用的工种数与未被录用的工种数的乘积,
则被录用的工种数是0、1、2、3,未被录用的工种数是3、2、1、0,
它们的乘积是0×3=0,1×2=2,2×1=2,3×0=0,
∴ξ的取值只能是0、2;
当ξ=0时,P(ξ=0)=0.16;
当ξ=2时,P(ξ=2)=0.84;
∴ξ的分布列为:
…(9分)
数学期望是Eξ=0×0.16+2×0.84=1.68.
P=1-(1-0.8)×(1-0.5)×(1-0.2)=1-0.2×0.5×0.8=0.92;
(2)设ξ表示该技术人员被录用的工种数与未被录用的工种数的乘积,
则被录用的工种数是0、1、2、3,未被录用的工种数是3、2、1、0,
它们的乘积是0×3=0,1×2=2,2×1=2,3×0=0,
∴ξ的取值只能是0、2;
当ξ=0时,P(ξ=0)=0.16;
当ξ=2时,P(ξ=2)=0.84;
∴ξ的分布列为:
| ξ | 0 | 2 | |
| P | 0.16 | 0.84 |
数学期望是Eξ=0×0.16+2×0.84=1.68.
点评:本题考查了相互独立事件的概率公式的应用问题,也考查了离散型随机变量的分布列与数学期望的应用问题,是中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=
如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=| 2 |
BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中不正确的是( )
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AB∥平面ABC |
设f(x)=|xex|,若关于x的方程(1-t)f2(x)-f(x)+t=0有四个不同的实数根,则实数t的取值范围为( )
| A、(-∞,0) | ||
B、(0,
| ||
C、(
| ||
| D、(1,+∞) |
等比数列{an}的首项a1=1002,公比q=
,记Pn=a1•a2•…•an,则Pn达到最大值时,n的值为( )
| 1 |
| 2 |
| A、8 | B、9 | C、10 | D、11 |
函数f(x)=sinx+cos2x的图象为( )
A、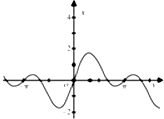 |
B、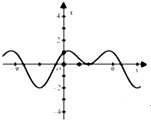 |
C、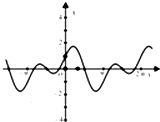 |
D、 |
