题目内容
等比数列{an}共有2n项，它的全部各项和是奇数项和的3倍，则公比q= ．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：设首项为a1，公比为q（q≠1），根据所有项的和是奇数项和的3倍，建立方程，即可求出q．
解答：
解：设首项为a1，公比为q（q≠1），则
∵所有项的和是奇数项和的3倍，
∴
=3×
，
∴q=2，
故答案为：2．
∵所有项的和是奇数项和的3倍，
∴
| a1(1-q2n) |
| 1-q |
| a1(1-q2n) |
| 1-q2 |
∴q=2，
故答案为：2．
点评：本题考查等比数列的通项与求和，考查学生的计算能力，属于中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
已知复数z满足（1-i）z=2，则|
|为（ ）
. |
| z |
| A、1+i | ||
| B、1-i | ||
C、
| ||
| D、2 |
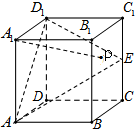如图所示，在长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，AA1=3，E是棱CC1上的点，且| CE |
| 1 |
| 3 |
| CC1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
化（
） -
的结果是（ ）
| 27 |
| 125 |
| 1 |
| 3 |
| A、3 | ||
| B、5 | ||
C、
| ||
D、
|