题目内容
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),过点P(-2,-4)的直线l:
(t为参数)与C交于M,N两点.
(1)求曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
|
(1)求曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)把
代入ρsin2θ=2acosθ,由
,消去参数t可得所求;(2)将
代入y2=2ax并整理可得t得二次方程,由韦达定理可得t1+t2和t1•t2的值,由等比中项可得|MN|2=|PM|•|PN|,整体代入可得a得方程,解方程可得.
|
|
|
解答:
解:(1)把
代入ρsin2θ=2acosθ(a>0)得y2=2ax,(a>0),
由l:
,消去参数t可得x-y-2=0,
∴曲线C和直线l的普通方程分别是y2=2ax,(a>0),x-y-2=0;
(2)将
代入y2=2ax并整理可得t2-2
(4+a)t+8(4+a)=0,
由韦达定理可得t1+t2=2
(4+a),t1•t2=8(4+a),
∵|PM|,|MN|,|PN|成等比数列,
∴|MN|2=|PM|•|PN|,
∴(t1-t2)2=(t1+t2)2-4t1•t2=t1•t2,
∴8(4+a)2-4×8(4+a)=8(4+a),解得a=1
|
由l:
|
∴曲线C和直线l的普通方程分别是y2=2ax,(a>0),x-y-2=0;
(2)将
|
| 2 |
由韦达定理可得t1+t2=2
| 2 |
∵|PM|,|MN|,|PN|成等比数列,
∴|MN|2=|PM|•|PN|,
∴(t1-t2)2=(t1+t2)2-4t1•t2=t1•t2,
∴8(4+a)2-4×8(4+a)=8(4+a),解得a=1
点评:本题考查直线的参数方程和极坐标方程,属基础题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
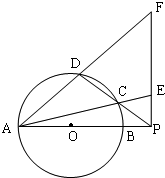 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P做AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P做AP的垂线,交直线AC于点E,交直线AD于点F.(1)求证:∠PEC=∠PDF;
(2)求PE•PF的值.
设集合A={x|1<x<5},B={x|x2-2x-3≤0},则A∩(∁RB)=( )
| A、(1,5) |
| B、(3,5) |
| C、(1,3) |
| D、(1,2) |
平面区域
的面积是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
设x、y、z是正数,且x2+4y2+9z2=4,2x+4y+3z=6,则x+y+z等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
与双曲线2y2-x2=4焦距不同的是( )
| A、2x2-y2=4 |
| B、y2-x2=3 |
| C、x2+4y2=8 |
| D、2y2+x2=6 |