题目内容

已知a、b、c分别为△ABC三个内角A、B、C的对边，若（c-b）sinC=asinA-bsinB，则∠A=
 
．
考点：余弦定理
专题：三角函数的求值
分析：已知等式利用正弦定理化简得到关系式，再利用余弦定理表示出cosA，将关系式代入计算求出cosA的值，即可确定出A的度数．
解答： 解：已知等式利用正弦定理化简得：c（c-b）=a2-b2，即b2+c2-a2=bc，
∴cosA=
b2+c2-a2
2bc
=
bc
2bc
=
1
2
，
∵∠A为三角形内角，
∴∠A=
π
3
．
故答案为：
π
3
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
在△ABC中，a，b，c分别为角A，B，C的对边，且角A=60°，若S△ABC=
15
3
4
，且5sinB=3sinC，则△ABC的周长等于
 
．
把5名新兵分配到一、二、三3个不同的班，要求每班至少有一名且甲必须分配在一班，则所有不同的分配种数为
 
．
若奇函数满足f（x+3）=f（x）+f（-3）则f(
3
2
)=
 
．
若关于x的不等式a（x2+x+4）≥|x|对任意实数x都成立，则实数a的取值范围是
 
．
若集合A={x|
1
x
＜1}，B={x||x|＜2}，则A∩B=
 
．
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：ρsin2θ=2acosθ（a＞0），过点P（-2，-4）的直线l：
x=-2+
2
2
t
y=-4+
2
2
t
（t为参数）与C交于M，N两点．
（1）求曲线C和直线l的普通方程；
（2）若|PM|，|MN|，|PN|成等比数列，求实数a的值．
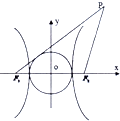如图，点P在双曲线
x2
a2
-
y2
b2
=1的右支上，F1，F2分别是双曲线的左右焦点，|PF2|=|F1F2|，直线PF1与圆x2+y2=a2相切，则双曲线的离心率e（　　）
A、
4
3
B、
5
3
C、
3
D、2
设点P（x，y）满足不等式组
x+y≤1
x-y+1≥0
y≥0
，则f（x，y）=x+y-10的最大值和最小值分别为（　　）
A、-9，-11
B、-11
2
，-9
C、-11
2
，-9
2
D、9
2
，-11

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网