题目内容
设x、y、z是正数,且x2+4y2+9z2=4,2x+4y+3z=6,则x+y+z等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:二维形式的柯西不等式
专题:不等式的解法及应用
分析:运用柯西不等式:(a2+b2+c2)(d2+e2+f2)≥(ad+be+cf)2,当且仅当
=
=
等号成立.
| a |
| d |
| b |
| e |
| c |
| f |
解答:
解:∵x、y、z是正数,x2+4y2+9z2=4,2x+4y+3z=6,
∴(22+22+12)(x2+4y2+9z2)=9×4≥(2x+4y+3z)2=36,
∴可设
=
=
=k,(k为常数),代入2x+4y+3z=6,
得k=
,
∴x+y+z=
+
+
=
.
故选A.
∴(22+22+12)(x2+4y2+9z2)=9×4≥(2x+4y+3z)2=36,
∴可设
| 2 |
| x |
| 2 |
| 2y |
| 1 |
| 3z |
得k=
| 3 |
| 2 |
∴x+y+z=
| 2 |
| k |
| 2 |
| k |
| 1 |
| 3k |
| 20 |
| 9 |
故选A.
点评:本题考查三元柯西不等式及应用,考查基本的运算能力,是一道基础题.

练习册系列答案
相关题目
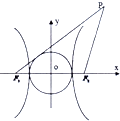 如图,点P在双曲线
如图,点P在双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
使函数f(x)=
在(-∞,+∞)上是减函数的一个充分不必要条件是( )
|
A、
| ||||
B、0<a<
| ||||
C、
| ||||
D、0<a<
|
已知命题p:函数f(x)=|sin2x-
|的最小正周期为π;命题q:若函数f(x+1)为偶函数,则f(x)关于x=1对称.则下列命题是真命题的是( )
| 1 |
| 2 |
| A、p∧q |
| B、p∨q |
| C、(¬p)∧(¬q) |
| D、p∨(¬q) |
某几何体的三视图如图所示,则该几何体的体积是( )


A、
| ||
B、
| ||
| C、6π | ||
D、8+
|
设点P(x,y)满足不等式组
,则f(x,y)=x+y-10的最大值和最小值分别为( )
|
| A、-9,-11 | ||||
B、-11
| ||||
C、-11
| ||||
D、9
|
方程3x+1-x=6的解所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |