题目内容
已知p：（
）2≤4，q：x2-2x+1-m2≤0（m＞0）．
（1）分别求出命题p、命题q所表示的不等式的解集A，B；
（2）若￢p是￢q的必要不充分条件，求实数m的取值范围．
| x-4 |
| 3 |
（1）分别求出命题p、命题q所表示的不等式的解集A，B；
（2）若￢p是￢q的必要不充分条件，求实数m的取值范围．
考点：复合命题的真假
专题：不等式的解法及应用,简易逻辑
分析：（1）解二次不等式即可，
（2）运用充分必要条件与集合的包含关系，得出不等式求解即可．
（2）运用充分必要条件与集合的包含关系，得出不等式求解即可．
解答：
解：（1）∵p：（
）2≤4，q：x2-2x+1-m2≤0（m＞0）．
∴A={x|-2≤x≤10}，B={x|x2-2x+1-m2≤0（m＞0）}={x|1-m≤x≤1+m}
（2）∵￢p是￢q的必要不充分条件
∴q是p的必要不充分条件，
令p命题对应的集合为P，q对应的集合为Q，
即P?Q，
在1+m≥10，且1-m≤-2，
即m≥9且m≥3，
所以m≥9
故实数m的取值范围：m≥9
| x-4 |
| 3 |
∴A={x|-2≤x≤10}，B={x|x2-2x+1-m2≤0（m＞0）}={x|1-m≤x≤1+m}
（2）∵￢p是￢q的必要不充分条件
∴q是p的必要不充分条件，
令p命题对应的集合为P，q对应的集合为Q，
即P?Q，
在1+m≥10，且1-m≤-2，
即m≥9且m≥3，
所以m≥9
故实数m的取值范围：m≥9
点评：本题考查了复合命题，充分必要条件与集合的包含关系，属于容易题．
练习册系列答案
阅读快车系列答案
相关题目
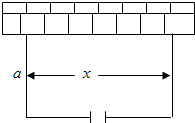某动物园要围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：元）．