题目内容
5．已知$\frac{1+cos2α}{sin2α}=\frac{1}{2}$，则tanα=（ ）| A． | 2 | B． | 3 | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
分析 由条件利用同角三角函数的基本关系，二倍角公式，即可计算得解．
解答 解：∵$\frac{1+cos2α}{sin2α}=\frac{1}{2}$，可得：$\frac{2co{s}^{2}α}{2sinαcosα}$=$\frac{cosα}{sinα}$=$\frac{1}{tanα}$=$\frac{1}{2}$，
∴解得：tanα=2．
故选：A．
点评 本题主要考查同角三角函数的基本关系，二倍角公式在三角函数化简求值中的应用，属于基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
15．要使圆x2+y2+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧，则有（ ）
| A． | D2+E2-4F＞0，且F＜0 | B． | D＜0，F＞0 | ||
| C． | D≠0，F≠0 | D． | F＜0 |
在四边形ABCD中，已知BC=2，DC=4，且∠A：∠ABC：∠C：∠ADC=3：7：4：10
10．
在函数y=|x|（x∈[-2，2]）的图象上有一点P（t，|t|），此函数的图象与x轴、直线x=-2及x=t围成的图形（如图阴影部分）的面积为S，则S与t的函数关系可表示为（ ）
在函数y=|x|（x∈[-2，2]）的图象上有一点P（t，|t|），此函数的图象与x轴、直线x=-2及x=t围成的图形（如图阴影部分）的面积为S，则S与t的函数关系可表示为（ ）| A． |  | B． |  | C． |  | D． |  |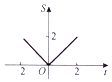
17．设F1，F2是双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的两个焦点，点P在双曲线上，且∠F1PF2=60°，则|PF1||PF2|的值为（ ）
| A． | 36 | B． | 16$\sqrt{3}$ | C． | 16 | D． | 64 |
15．在△ABC中，角A，B，C的对边分别是a，b，c，且满（2a-c）cosB=bcosC，则A的取值范围（ ）
| A． | （0，$\frac{2π}{3}$） | B． | （0，π） | C． | （$\frac{π}{3}$，$\frac{2π}{3}$） | D． | （$\frac{2π}{3}$π） |