题目内容
15.要使圆x2+y2+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧,则有( )| A. | D2+E2-4F>0,且F<0 | B. | D<0,F>0 | ||
| C. | D≠0,F≠0 | D. | F<0 |
分析 令y=0,则圆的方程为x2+Dx+F=0,将圆与x轴的相交问题,转化为方程x2+Dx+F=0的解的情况分析,根据一元二次方程的根与系数的关系,分析可得答案.
解答 解:∵x2+y2+Dx+Ey+F=0表示圆,则D2+E2-4F>0.
令y=0,则圆的方程为x2+Dx+F=0,
当D2>4F时,即方程有两解时,
则这个方程的两根为该圆与x轴的交点的横坐标,
根据题意,要求该圆与x轴的两个交点分别位于原点的两侧,
由根与系数的关系,有F<0,
且满足D2>4F,方程有两解的条件,
故选:A.
点评 本题考查圆的方程综合运用,注意圆与坐标轴的交点,可以令x或y的值为0,即可求得其与坐标轴交点的情况

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12.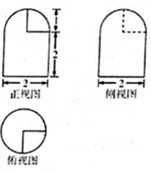 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )
 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{25}{4}$π | B. | 7π | C. | $\frac{29}{4}$π | D. | $\frac{31}{4}$π |
7.若对?a∈[$\frac{1}{{e}^{2}}$,1],?b∈[-1,1],使λ+alna=2b2eb(e是自然对数的底数),则实数λ的取值范围是( )
| A. | [$\frac{1}{e}$,2e] | B. | [$\frac{1}{e}$,$\frac{2}{e}$] | C. | [$\frac{3}{e}$,2e] | D. | [$\frac{3}{e}$,$\frac{8}{{e}^{2}}$] |
5.已知$\frac{1+cos2α}{sin2α}=\frac{1}{2}$,则tanα=( )
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
 如图所示的多面体ABCDEF,四边形ABCD是边长为2的正方形,面BDFE⊥面ABCD,四边形BDFE为矩形,BE长为a,M为AE的中点,AC∩BD=O.
如图所示的多面体ABCDEF,四边形ABCD是边长为2的正方形,面BDFE⊥面ABCD,四边形BDFE为矩形,BE长为a,M为AE的中点,AC∩BD=O.