题目内容
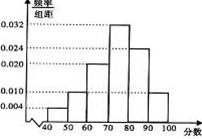 某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.
某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.(1)请估计该校这20个班级中成绩不低于60分的人数;
(2)为了帮助学生提高数学成绩,该班班主任决定成立“二帮一”小组:对成绩在[40,50)内的每位同学,从成绩在[90,100]中选两位同学对其数学学习提供帮助,各组成员没有重复.已知甲成绩为42分,乙成绩为95分,求甲、乙恰好被安排在同一小组的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)根据频率分布直方图,成绩不低于60分的频率,然后根据频数=频率×总数可求出所求;
(2)先算出成绩在[40,50)分数段内的人数,以及成绩在[90,100]分数段内的人数,列出所有的“二帮一”小组分组办法的基本事件,以及甲、乙两同学被分在同一小组的基本事件,最后利用古典概型的概率公式解之即可.
(2)先算出成绩在[40,50)分数段内的人数,以及成绩在[90,100]分数段内的人数,列出所有的“二帮一”小组分组办法的基本事件,以及甲、乙两同学被分在同一小组的基本事件,最后利用古典概型的概率公式解之即可.
解答:
解:(1)根据频率分布直方图,
成绩不低于60分的频率为1-10×(0.004+0.010)=0.86.
由于该校高一年级共有学生50×20=1000人,
利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于60分的人数为1000×0.86=860人.
(2)成绩在[40,50)分数段内的人数为50×0.04=2人
成绩在[90,100)分数段内的人数为50×0.1=5人,
将[40,50)内2人记为甲、A.[90,100)内5人记为乙、B、C、D、E.
“二帮一”小组有以下20种分组办法:
甲乙B,甲乙C,甲乙D,甲乙E,甲BC,甲BD,甲BE,甲CD,甲CE,甲DE,
A乙B,A乙C,A乙D,A乙E,
ABC,ABD,ABE,
ACD,ACEE,
ADE,
其中甲、乙两同学被分在同一小组有4种办法:甲乙B,甲乙C,甲乙D,甲乙E
所以甲乙两同学恰好被安排在同一小组的概率为P=
=
.
成绩不低于60分的频率为1-10×(0.004+0.010)=0.86.
由于该校高一年级共有学生50×20=1000人,
利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于60分的人数为1000×0.86=860人.
(2)成绩在[40,50)分数段内的人数为50×0.04=2人
成绩在[90,100)分数段内的人数为50×0.1=5人,
将[40,50)内2人记为甲、A.[90,100)内5人记为乙、B、C、D、E.
“二帮一”小组有以下20种分组办法:
甲乙B,甲乙C,甲乙D,甲乙E,甲BC,甲BD,甲BE,甲CD,甲CE,甲DE,
A乙B,A乙C,A乙D,A乙E,
ABC,ABD,ABE,
ACD,ACEE,
ADE,
其中甲、乙两同学被分在同一小组有4种办法:甲乙B,甲乙C,甲乙D,甲乙E
所以甲乙两同学恰好被安排在同一小组的概率为P=
| 4 |
| 20 |
| 1 |
| 5 |
点评:本题主要考查频率、频数、统计和概率等知识,考查数形结合、化归与转化的数学思想方法,以及运算求解能力.属于中档题.

练习册系列答案
相关题目
设函数f(x)=
,则f(log23)=( )
|
|
| A、13 | B、19 | C、37 | D、49 |
已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1且cosA=
,则△ABC的外接圆的直径等于( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|