题目内容

已知正方体ABCD-A1B1C1D1的各顶点都在同一球面上，若四面体A-B1CD1的表面积为8
3
，则球的体积为
 
．
考点：球的体积和表面积
专题：球
分析：画出正方体，通过正四面体求出正四面体的棱长，然后求出正方体的棱长，求出外接球的半径，即可求解球O的表面积．
解答： 解：如图：四面体A-B1CD1是正四面体，表面积为8
3
，
∴一个面的面积为2
3
，
∴正方体的对角线的长AC满足：
3
4
AC2=2
3
，
∴AC=2
2
，
∴AB=2，
正方体的对角线就是外接球的直径，2R=2
3
，
∴R=
3
，
球的体积为
4π
3
R3=4
3
π．
故答案为：4
3
π．
点评：本题考查正方体以及正四面体的外接球的体积的求法，求出外接球的半径是解题的关键，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
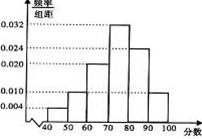某校高三年级发展均衡，各班均有学生50人，全校共有20个平行班级．随机选择一个班，将他们的期中数学考试成绩分成六段：[40，50），[50，60），…，[90，100]，得到如图所示频率分布直方图．
（1）请估计该校这20个班级中成绩不低于60分的人数；
（2）为了帮助学生提高数学成绩，该班班主任决定成立“二帮一”小组：对成绩在[40，50）内的每位同学，从成绩在[90，100]中选两位同学对其数学学习提供帮助，各组成员没有重复．已知甲成绩为42分，乙成绩为95分，求甲、乙恰好被安排在同一小组的概率．
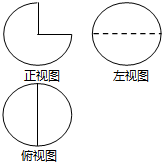一个几何体的三视图如图所示，其中俯视图与左视图均为半径是2的圆，则这个几何体的表面积是
 
．
已知直线l，m，平面α，β，γ，给出下列命题：
①l∥α，l∥β，α∩β=m，则l∥m  
②α∥β，β∥γ，m⊥α，则m⊥β
③α⊥γ，β⊥γ，则α⊥β  
④l⊥m，l⊥α，m⊥β，则α⊥β
其中正确的命题的序号是
 
．
已知数列{an}中，a1=1，a2n=n-an，a2n+1=an+1，则a1+a2+a3+…+a99=
 
．
若在（x+1）4（ax-1）2的展开式中x的系数是6，则a=
 
．
（文）已知向量
a
=（-3，-4），
b
=（0，1），点C对应的向量
c
=
a
+λ
b
，且C点在函数y=cos
π
3
x的图象上，则实数λ=
 
．
若将函数y=sin2x的图象向右平移φ（φ＞0）个单位，得到的图象关于直线x=
π
6
对称，则φ的最小值为
 
．
函数y=sin（2x+
π
3
）的图象经过下列平移，可以得到偶函数图象的是（　　）
A、向右平移
π
6
个单位
B、向左平移
π
6
个单位
C、向右平移
5π
12
个单位
D、向左平移
5π
12
个单位

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网