题目内容
设函数f(x)=
,则f(log23)=( )
|
|
| A、13 | B、19 | C、37 | D、49 |
考点:函数的值
专题:函数的性质及应用
分析:根据积分公式将函数进行化简,然后利用对数的基本运算代入即可得到结论.
解答:
解:当x≥4时,f(x)=2x+3(
x
-
x3)|
=2x+3×(
-
)=2x+1,
∵1<log23<2,
∴5<log23+4<6,
即f(log23)=f(log23+4)=f(log248)=2log248+1=48+1=49,
故选:D.
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
1 0 |
| 2 |
| 3 |
| 1 |
| 3 |
∵1<log23<2,
∴5<log23+4<6,
即f(log23)=f(log23+4)=f(log248)=2log248+1=48+1=49,
故选:D.
点评:本题主要考查函数值的计算,利用分段函数的表达式是解决本题的关键,比较基础.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0),作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若
=2
-
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
| OP |
| OE |
| OF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则这个球的体积是( )
已知一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则这个球的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若满足条件
的点P(x,y)构成三角形区域,则实数k的取值范围是( )
|
| A、(1,+∞) |
| B、(0,1) |
| C、(-1,1) |
| D、(-∞,-1)∪(1,+∞) |
将一颗骰子连续抛掷三次,已知它落地时向上的点数恰好依次成等差数列,那么这三次抛掷向上的点数之和为12的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
log212-log23=( )
| A、-2 | ||
| B、0 | ||
C、
| ||
| D、2 |
若
,则目标函数z=
的取值范围是( )
|
| x+2y |
| x |
| A、[2,5] | ||
| B、[1,5] | ||
C、[
| ||
| D、[2,6] |
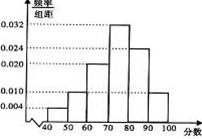 某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.
某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.