题目内容
已知函数fn(x)=x+
,(x>0,n≥1,n∈Z),以点(n,fn(n))为切点作函数y=fn(x)图象的切线ln,记函数y=fn(x)图象与三条直线x=n,x=n+1,ln所围成的区域面积为an.
(Ⅰ)求an;
(Ⅱ)求证:an<
;
(Ⅲ)设Sn为数列{an}的前n项和,求证:Sn<
.
| n |
| x |
(Ⅰ)求an;
(Ⅱ)求证:an<
| 1 |
| 3n2 |
(Ⅲ)设Sn为数列{an}的前n项和,求证:Sn<
| 5 |
| 9 |
考点:数列与不等式的综合,定积分
专题:综合题,压轴题,点列、递归数列与数学归纳法
分析:(Ⅰ)求出原函数的导函数,求出切点坐标,由直线方程的点斜式求得切线方程,由定积分求得函数y=fn(x)图象与三条直线x=n,x=n+1,ln所围成的区域面积为an;
(Ⅱ)要证明an<
,即证明nln(1+
)+
-1<
,可设想构造函数h(x)=ln(1+x)-x+
x2-
x3 (x≥0),由其导函数确定原函数的单调性,进一步得到ln(1+x)<x-
x2+
x3成立,取x=
,然后不等式两边同时乘以n,则可证得an<
;
(Ⅲ)法一、由(Ⅱ)中不等式进一步放缩得到an<
<
•
=
•(
-
),把数列
{an}求和后正负项相消可证明不等式;
法二、把数列{an}的前n项和的前两项作和,然后由
<
=
=
(
-
)放大n≥3的项,可证明n≥3时Sn<
,单独验证S1,S2后可得答案.
(Ⅱ)要证明an<
| 1 |
| 3n2 |
| 1 |
| n |
| 1 |
| 2n |
| 1 |
| 3n2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 3n2 |
(Ⅲ)法一、由(Ⅱ)中不等式进一步放缩得到an<
| 1 |
| 3n2 |
| 1 |
| 3 |
| 1 | ||
n2-
|
| 2 |
| 3 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
{an}求和后正负项相消可证明不等式;
法二、把数列{an}的前n项和的前两项作和,然后由
| 1 |
| n2 |
| 1 |
| n2-1 |
| 1 |
| (n-1)(n+1) |
| 1 |
| 2 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 5 |
| 9 |
解答:
(Ⅰ)解:由fn(x)=x+
,得fn′(x)=1-
,
切点为(n,n+1),则切线ln方程为y-(n+1)=(1-
)(x-n),
即ln:y=(1-
)x+2,
∴an=
[x+
-(1-
)x-2]dx=
(
+
-2)dx=nln(1+
)+
-1;
(Ⅱ)证明:构造函数h(x)=ln(1+x)-x+
x2-
x3 (x≥0),
则h′(x)=
-1+x-x2=
≤0
即函数h(x)=ln(1+x)-x+
x2-
x3 (x≥0)单调递减,而h(0)=0,
∴h(x)≤0,等号在x=0时取得,
∴当x>0时,ln(1+x)<x-
x2+
x3成立,
∴知ln(1+
)<
-
(
)2+
(
)3
∴an=nln(1+
)+
-1<
;
(Ⅲ)证明:
法一、
∵an<
<
•
=
•(
-
),
∴当n=1时,Sn=a1=
<
;
当n≥2时,Sn=
ak=a1+
ak<
+
(
-
+
-
+…+
-
)
=
-
•
<
.
方法二、
由(Ⅱ)知an<
,
∴Sn=a1+a2+a3+…+an<
+
+
+…+
=
(
+
+
+…+
)=
(
+
+…+
),
∵
<
=
=
(
-
)(n≥3,n∈N*)
∴Sn<
[
+
(
-
)+
(
-
)+
(
-
)+…+
(
-
)]
=
[
+
(
+
-
-
)]=
-
(
+
)<
又S1=a1=
<
,S2=a1+a2≤
+
=
<
,
∴综上所述:对一切n∈N*,都有Sn<
.
| n |
| x |
| n |
| x2 |
切点为(n,n+1),则切线ln方程为y-(n+1)=(1-
| n |
| n2 |
即ln:y=(1-
| 1 |
| n |
∴an=
| ∫ | n+1 n |
| n |
| x |
| 1 |
| n |
| ∫ | n+1 n |
| x |
| n |
| n |
| x |
| 1 |
| n |
| 1 |
| 2n |
(Ⅱ)证明:构造函数h(x)=ln(1+x)-x+
| 1 |
| 2 |
| 1 |
| 3 |
则h′(x)=
| 1 |
| 1+x |
| -x3 |
| 1+x |
即函数h(x)=ln(1+x)-x+
| 1 |
| 2 |
| 1 |
| 3 |
∴h(x)≤0,等号在x=0时取得,
∴当x>0时,ln(1+x)<x-
| 1 |
| 2 |
| 1 |
| 3 |
∴知ln(1+
| 1 |
| n |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| 3 |
| 1 |
| n |
∴an=nln(1+
| 1 |
| n |
| 1 |
| 2n |
| 1 |
| 3n2 |
(Ⅲ)证明:
法一、
∵an<
| 1 |
| 3n2 |
| 1 |
| 3 |
| 1 | ||
n2-
|
| 2 |
| 3 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴当n=1时,Sn=a1=
| 1 |
| 3 |
| 5 |
| 9 |
当n≥2时,Sn=
| n |
 |
| k=1 |
| n |
 |
| k=2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 5 |
| 9 |
| 2 |
| 3 |
| 1 |
| 2n+1 |
| 5 |
| 9 |
方法二、
由(Ⅱ)知an<
| 1 |
| 3n2 |
∴Sn=a1+a2+a3+…+an<
| 1 |
| 3×12 |
| 1 |
| 3×22 |
| 1 |
| 3×32 |
| 1 |
| 3n2 |
=
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 3 |
| 5 |
| 4 |
| 1 |
| 32 |
| 1 |
| n2 |
∵
| 1 |
| n2 |
| 1 |
| n2-1 |
| 1 |
| (n-1)(n+1) |
| 1 |
| 2 |
| 1 |
| n-1 |
| 1 |
| n+1 |
∴Sn<
| 1 |
| 3 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| n-1 |
| 1 |
| n+1 |
=
| 1 |
| 3 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 5 |
| 9 |
| 1 |
| 6 |
| 1 |
| n |
| 1 |
| n+1 |
| 5 |
| 9 |
又S1=a1=
| 1 |
| 3 |
| 5 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3×22 |
| 5 |
| 12 |
| 5 |
| 9 |
∴综上所述:对一切n∈N*,都有Sn<
| 5 |
| 9 |
点评:本题考查了数列与不等式的综合,考查了定积分,训练了裂项相消法求数列的和,考查了放缩法求证不等式,
对于(Ⅱ)的证明,构造函数h(x)=ln(1+x)-x+
x2-
x3 (x≥0)是难点,证明(Ⅲ)的关键是对每一项的放缩,是难度较大的题目.
对于(Ⅱ)的证明,构造函数h(x)=ln(1+x)-x+
| 1 |
| 2 |
| 1 |
| 3 |

练习册系列答案
相关题目
将一颗骰子连续抛掷三次,已知它落地时向上的点数恰好依次成等差数列,那么这三次抛掷向上的点数之和为12的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
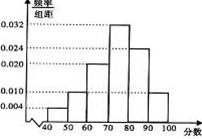 某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.
某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.