题目内容
设函数f(x)=ax-2-lnx(a∈R).
(Ⅰ)若f(x)在点(e,f(e))处的切线为x-ey-2e=0,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)当x>0时,求证:f(x)-ax+ex>0.
(Ⅰ)若f(x)在点(e,f(e))处的切线为x-ey-2e=0,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)当x>0时,求证:f(x)-ax+ex>0.
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)求出函数f(x)的导数并求出切点,运用点斜式方程写出切线方程并化为一般式,对照条件求出a;
(Ⅱ)求出导数f'(x),对a讨论,分a≤0,a>0,分别求出单调区间,注意定义域:(0,+∞);
(Ⅲ)运用分析法证明:f(x)-ax+ex>0.首先化简左边并构造函数:g(x)=ex-lnx-2(x>0),只需要证明g(x)>0,通过导数g'(x)的单调性,运用零点存在定理证明g'(x)在(0,+∞)上有唯一零点,设为t,由导函数g'(x)的单调性,得到g'(x)在(0,t)上小于0,在(t,+∞)上大于0,从而得到g(x)在x>0上的单调性,从而得出g(x)的极小值也是最小值g(t),证明g(t)不小于0,由
<t<1得g(t)>0,从而原不等式成立.
(Ⅱ)求出导数f'(x),对a讨论,分a≤0,a>0,分别求出单调区间,注意定义域:(0,+∞);
(Ⅲ)运用分析法证明:f(x)-ax+ex>0.首先化简左边并构造函数:g(x)=ex-lnx-2(x>0),只需要证明g(x)>0,通过导数g'(x)的单调性,运用零点存在定理证明g'(x)在(0,+∞)上有唯一零点,设为t,由导函数g'(x)的单调性,得到g'(x)在(0,t)上小于0,在(t,+∞)上大于0,从而得到g(x)在x>0上的单调性,从而得出g(x)的极小值也是最小值g(t),证明g(t)不小于0,由
| 1 |
| 3 |
解答:
解:(Ⅰ)∵f(x)=ax-2-lnx(x>0),
∴f'(x)=a-
=
,
又f(x)在点(e,f(e))处的切线为x-ey-2e=0,
∴f'(e)=a-
=
,故a=
;
(Ⅱ)由(Ⅰ)知,f'(x)=a-
=
(x>0),
当a≤0时,f'(x)<0在(0,+∞)上恒成立,
∴f(x)在(0,+∞)上是单调减函数,
当a>0时,令f'(x)=0,则x=
,
令f'(x)<0,则0<x<
,f'(x)>0,则x>
,
∴f(x)在(0,
)上单调递减,在(
,+∞)上单调递增,
综上可得:当a≤0时,f(x)的单调减区间为(0,+∞),
当a>0时,f(x)的单调减区间为(0,
),f(x)的单调增区间为(
,+∞);
(Ⅲ)当x>0时,要证f(x)-ax+ex>0,即证ex-lnx-2>0,
令g(x)=ex-lnx-2(x>0),只需证g(x)>0,
∵g'(x)=ex-
,由指数函数和幂函数的单调性知,g‘(x)在(0,+∞)上递增,
又g'(1)=e-1>0,g'(
)=e
-3<0,∴g'(1)•g'(
)<0,
∴g'(x)在(
,1)内存在唯一的零点,则g'(x)在(0,+∞)上有唯一零点,
设g'(x)的零点为t,则g'(t)=et-
=0,即et=
(
<t<1),
由g'(x)的单调性知:
当x∈(0,t)时,g'(x)<g'(t)=0,当x∈(t,+∞)时,g'(x)>g'(t)=0,
∴g(x)在(0,t)上为减函数,在(t,+∞)上为增函数,
∴当x>0时,g(x)≥g(t)=et-lnt-2=
-ln
-2=
+t-2≥2-2=0,
又
<t<1,等号不成立,∴g(x)>0,
∴当x>0时,f(x)-ax+ex>0.
∴f'(x)=a-
| 1 |
| x |
| ax-1 |
| x |
又f(x)在点(e,f(e))处的切线为x-ey-2e=0,
∴f'(e)=a-
| 1 |
| e |
| 1 |
| e |
| 2 |
| e |
(Ⅱ)由(Ⅰ)知,f'(x)=a-
| 1 |
| x |
| ax-1 |
| x |
当a≤0时,f'(x)<0在(0,+∞)上恒成立,
∴f(x)在(0,+∞)上是单调减函数,
当a>0时,令f'(x)=0,则x=
| 1 |
| a |
令f'(x)<0,则0<x<
| 1 |
| a |
| 1 |
| a |
∴f(x)在(0,
| 1 |
| a |
| 1 |
| a |
综上可得:当a≤0时,f(x)的单调减区间为(0,+∞),
当a>0时,f(x)的单调减区间为(0,
| 1 |
| a |
| 1 |
| a |
(Ⅲ)当x>0时,要证f(x)-ax+ex>0,即证ex-lnx-2>0,
令g(x)=ex-lnx-2(x>0),只需证g(x)>0,
∵g'(x)=ex-
| 1 |
| x |
又g'(1)=e-1>0,g'(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴g'(x)在(
| 1 |
| 3 |
设g'(x)的零点为t,则g'(t)=et-
| 1 |
| t |
| 1 |
| t |
| 1 |
| 3 |
由g'(x)的单调性知:
当x∈(0,t)时,g'(x)<g'(t)=0,当x∈(t,+∞)时,g'(x)>g'(t)=0,
∴g(x)在(0,t)上为减函数,在(t,+∞)上为增函数,
∴当x>0时,g(x)≥g(t)=et-lnt-2=
| 1 |
| t |
| 1 |
| et |
| 1 |
| t |
又
| 1 |
| 3 |
∴当x>0时,f(x)-ax+ex>0.
点评:本题是导数在函数中的综合运用,考查应用导数求曲线上某一点处的切线方程,求函数的单调区间,求函数的极值和最值,考查构造函数和分类讨论的数学思想方法,运用分析法证明不等式的重要方法,是一道综合题.

练习册系列答案
相关题目
若
,则目标函数z=
的取值范围是( )
|
| x+2y |
| x |
| A、[2,5] | ||
| B、[1,5] | ||
C、[
| ||
| D、[2,6] |
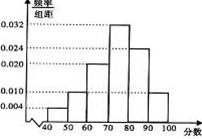 某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.
某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.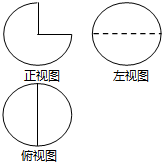 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是