题目内容
设函数f(x)=
•
,其中向量,x∈R.
=(sin2x,
),
=(-1,sin(2x-
))
(Ⅰ)求f(x)的最小值,并求使f(x)取得最小值的x的集合;
(Ⅱ)将函数f(x)的图象沿x轴向右平移,则至少平移多少个单位长度,才能使得到的函数g(x)的图象关于y轴对称?
| a |
| b |
| a |
| 3 |
| b |
| π |
| 6 |
(Ⅰ)求f(x)的最小值,并求使f(x)取得最小值的x的集合;
(Ⅱ)将函数f(x)的图象沿x轴向右平移,则至少平移多少个单位长度,才能使得到的函数g(x)的图象关于y轴对称?
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)利用平面向量的数量积的坐标运算可求得f(x)=sin(2x-
),从而可求得f(x)的最小值及f(x)取得最小值的x的集合;
(Ⅱ)依题意知,g(x)=sin(2x-2φ-
),利用2φ+
=kπ+
,可求得φ=
+
(k∈Z),又φ>0,从而可得φmin.
| π |
| 3 |
(Ⅱ)依题意知,g(x)=sin(2x-2φ-
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
解答:
解:(Ⅰ)f(x)=
•
=-sin2x+
sin(2x-
)
=
sin2x-
cos2x
=sin(2x-
).…..(4分)
∴函数f(x)的最小值为-1,此时2x-
=2kπ-
,解得x=kπ-
(k∈Z),
∴使f(x)取得最小值的x的集合为{x|x=kπ-
(k∈Z)}.…..(7分)
(Ⅱ)由条件可得g(x)=sin(2x-2φ-
),∵其图象关于y轴对称,
∴2φ+
=kπ+
,φ=
+
(k∈Z),又φ>0,
∴当k=0时,φ取得最小值
,
于是至少向右平移
个单位长度,才能使得到的函数g(x)的图象关于y轴对称.…..(12分)
| a |
| b |
=-sin2x+
| 3 |
| π |
| 6 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2x-
| π |
| 3 |
∴函数f(x)的最小值为-1,此时2x-
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
∴使f(x)取得最小值的x的集合为{x|x=kπ-
| π |
| 12 |
(Ⅱ)由条件可得g(x)=sin(2x-2φ-
| π |
| 3 |
∴2φ+
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
∴当k=0时,φ取得最小值
| π |
| 12 |
于是至少向右平移
| π |
| 12 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查正弦函数的对称性,考查平面向量的数量积的坐标运算,属于中档题.

练习册系列答案
相关题目
log212-log23=( )
| A、-2 | ||
| B、0 | ||
C、
| ||
| D、2 |
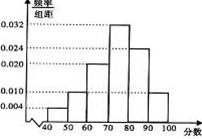 某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.
某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.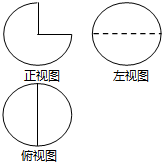 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是