题目内容
6.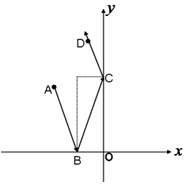 (1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;
(1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;(2)光线从点A(-3,4)射出,到x轴上的点B后,被x轴反射到y轴上的点C,又被y轴反射,这时反射光线恰好过点D(-1,6),求光线BC所在直线的斜率.
分析 (1)先根据A,B,P的坐标分别求得直线AP和BP的斜率,设L与线段AB交于M点,M由A出发向B移动,斜率越来越大,期间会出现AM平行y轴,此时无斜率.求得k的一个范围,过了这点M,斜率由-∞增大到直线BP的斜率K.求得k的另一个范围,最后综合可得答案
(2)先求点A关于x轴的对称点为A′,点D关于y轴的对称点为D′,直接连接A′D′的方程就是BC的方程
解答 解:(1)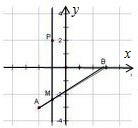 直线AP的斜率k=$\frac{-3-2}{-2+1}$=5
直线AP的斜率k=$\frac{-3-2}{-2+1}$=5
直线BP的斜率k=$\frac{0-2}{3+1}=-\frac{1}{2}$,
设L与线段AB交于M点,M由A出发向B移动,斜率越来越大,
在某点处会AM平行y轴,此时无斜率.即k≥5,
过了这点,斜率由-∞增大到直线BP的斜率-$\frac{1}{2}$.即k≤-$\frac{1}{2}$
直线l斜率取值范围为(-∞,-$\frac{1}{2}$]∪[5,+∞).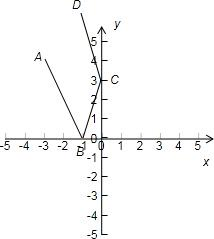 (2)点A关于x轴的对称点为
(2)点A关于x轴的对称点为
A′(-3,-4),
点D关于y轴的对称点为
D′(1,6),
由入射角等于反射角及对顶角相等可知A′、D′都在直线BC上,
∴BC的方程为5x-2y+7=0.
点评 本题主要考查了直线的斜率以及对称问题,解题的关键是利用了数形结合、转化思想,解题过程较为直观.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.已知曲线y=$\frac{x^2}{4}$-lnx的一条切线的斜率为-$\frac{1}{2}$,则切点的横坐标为( )
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
1.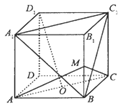 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )| A. | D1O∥平面A1BC1 | B. | D1O⊥平面MAC | ||
| C. | 异面直线BC1与AC所成的角为60° | D. | MO与底面所成角为90° |
16.函数f(x)=2x+5x的零点所在大致区间为( )
| A. | (0,1) | B. | (1,2) | C. | (-1,0) | D. | (-2,-1) |